Rayleigh Distribution

Back to: Random Testing

There are several situations where Rayleigh distribution occurs in random vibration. The peak amplitudes of a resonance‘s response to a random excitation exhibit a Rayleigh distribution. The amplitudes of the spatial vibration patterns in complex systems also have a Rayleigh distribution.

The second example led John W. Strutt to derive the formula for the Rayleigh probability distribution. He considered the vibration amplitude to be a vector r with a and b components that are independent and normally distributed with a zero mean value and variance, σ_o ².

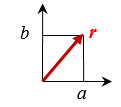
Equation 23 gives the normalized magnitude of r.

(1)  

Equation 23

Equation 24 gives the PDF, which is displayed in Figure 3.19.

(2)  

Equation 24

The Rayleigh PDF is not symmetrical, and the mean value is not equal to 1. Instead, r ≅ 1.25 σ_o and σ_r ≅ 0.655 σ_o.

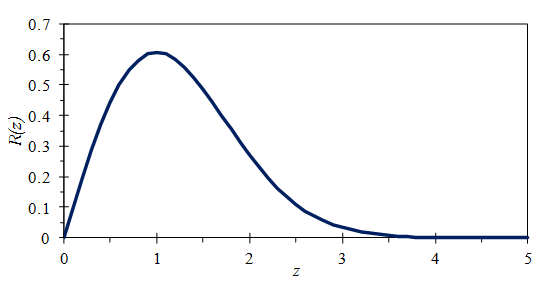
Figure 3.19. The Rayleigh distribution.

Example

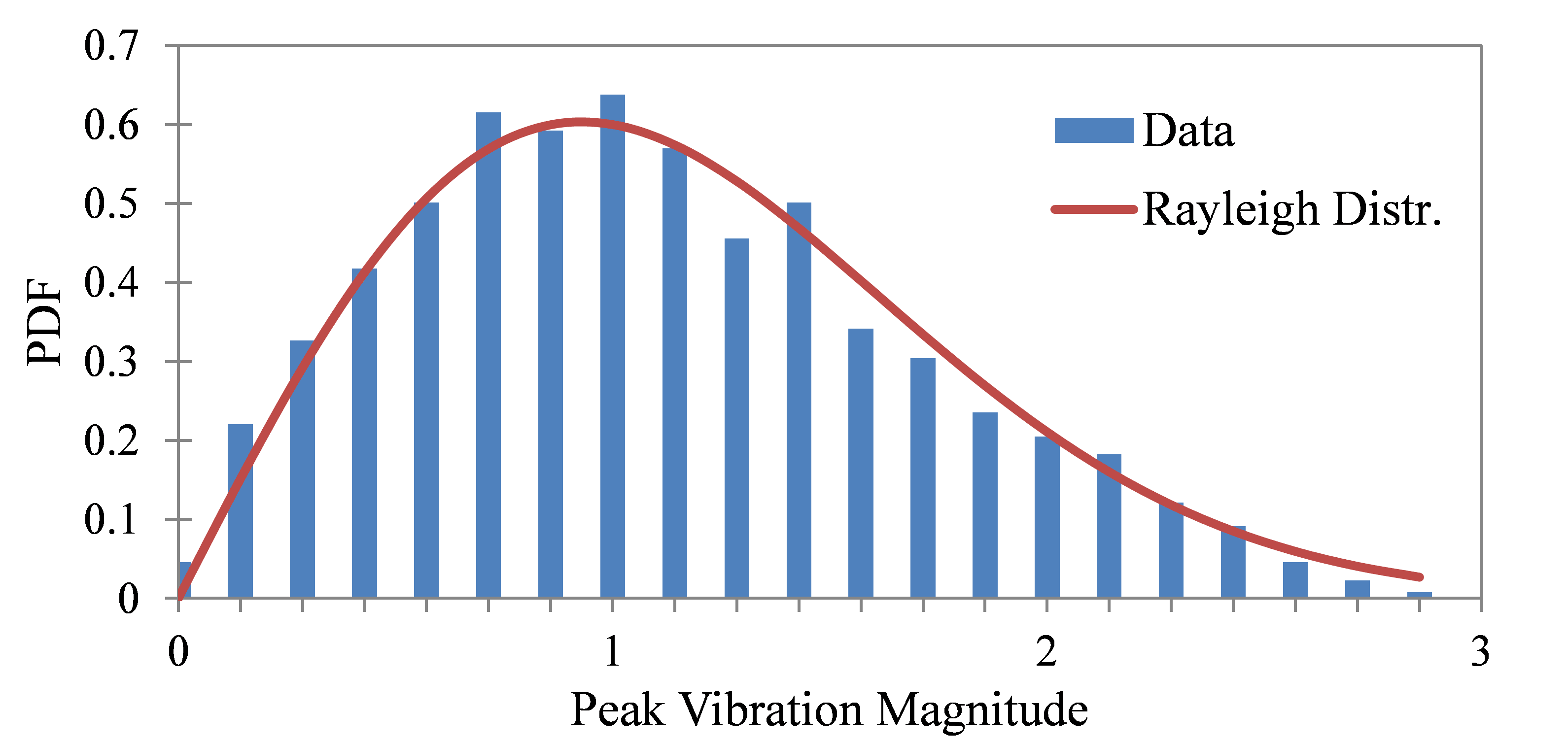
Figure 3.20 displays the vibration response of a cantilever beam’s resonance to random excitation at the base. Figure 3.21 compares the histogram of the peak magnitudes, |Ai|, to the Rayleigh distribution. The peak magnitudes are proportional to the peak stresses in the beam. Application-wise, engineers can use the results in fatigue analysis.

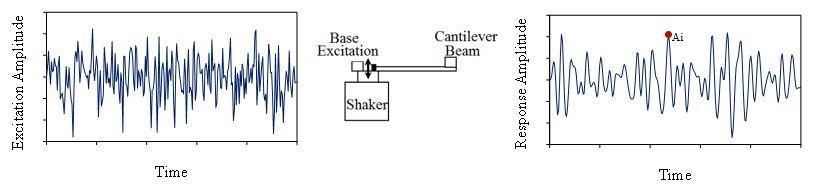
Figure 3.20. Random vibration response of the fundamental resonance of a cantilever beam.

Confidence Intervals

The Rayleigh distribution has a close association with the χ₂² distribution because the Rayleigh variables are the square root of the χ₂² variables.

(3)  

The area P in the graph below displays the confidence level “not to be exceeded” for the peak level estimation. Figure 3.22 is a plot as a function of the number of standard deviations from the mean.

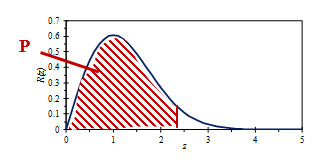
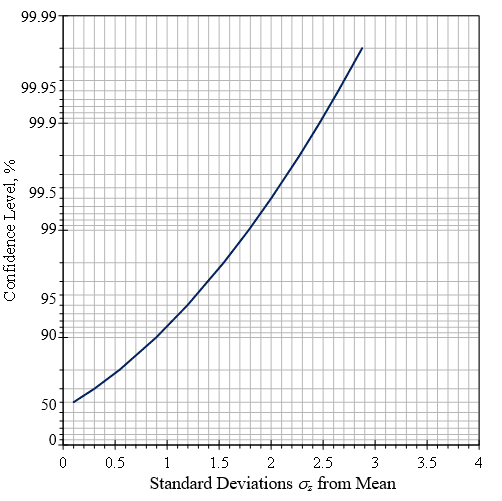
Figure 3.22. Confidence intervals for “not to exceed levels” with Rayleigh distribution.