Chi-Squared Distribution

March 29, 2018

Chi-squared ( $\chi^2$ ) distribution is the distribution of a sum of squared random variables. Among other applications, it can estimate the confidence interval for the variance of a random variable from a normal distribution.

A chi-squared distribution with N degrees of freedom ( $\chi^2_{N}$ ) determines the probability of a normal distribution where the mean value ( $\mu$ ) equals 0 and variance ( $\sigma^2$ ) equals 1.

Figure 3.14 is an example of the $\chi^2_{N}$ probability density function (PDF) for different values of N. As N approaches infinity, the $\chi^2_{N}$ distribution converges with the normal distribution. For all the $\chi^2_{N}$ distributions, the mean value is μ = N, and the variance is σ² = 2.

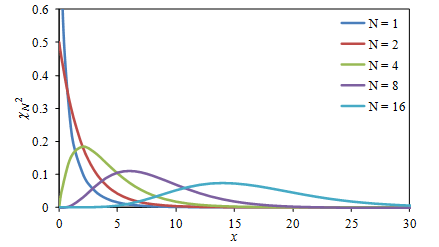
$chi^2_{N} distribution for the sum of N values of x2$

Figure 3.14. $\chi^2_{N}$ distribution for the sum of N values of x2.

Equation 16 is the PDF formula, where Γ is the Gamma function.

(1) $\begin{equation*} \chi^2_{N} = \frac {x^{(\frac{N}{2} - 1)}e^{-\frac {x}{2}}} {2^\frac{N}{2} \Gamma (\frac{N}{2})} \end{equation*}$

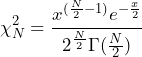
Equation 16

The squared values that evaluate the mean-square are $\chi^2_{1}$ distributed. Figure 3.15 illustrates this using the car vibration signal in Figure 3.2. The distribution is strongly biased toward small values as shown by the simplified formula for $\chi^2_{1}$ (Equation 17).

(2) $\begin{equation*} \chi^2_{1} = \frac {1}{\sqrt{2\pi x}}e^{-\frac{x}{2}} \end{equation*}$

Equation 17

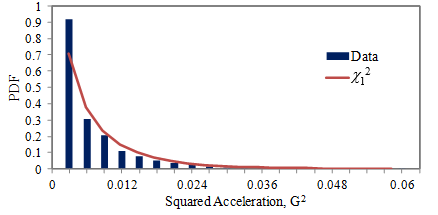
$PDF of squared car vibration data from Figure 3.2 compared to chi^2_{1}$

Figure 3.15. PDF of squared car vibration data from Figure 3.2 compared to $\chi^2_{1}$ .

Confidence Intervals

Variance is derived from the mean-square value. Therefore, $\chi^2_{N}$ distribution can determine the confidence interval for the variance.

For a random variable x with a standard deviation of σ_x, the summation of N values-squared has a σ_x²χ₁² distribution. Therefore, the variance has a σ_x²χ₁²/N distribution.

The $\chi^2_{N}$ distributions are not symmetrical, so the estimated confidence intervals for the variance are not symmetrical. In Figure 3.16, the values of $N / \chi^2_{N}$ are on a plot versus N for different confidence levels. The confidence interval for the variance is then stated as the interval:

(3) $\begin{equation*} \left(\frac {N\sigma^2_{x}}{\chi^2_{lower}}, \frac {N\sigma^2_{x}}{\chi^2_{upper}}\right), \text {with the appropriate e confidence level} \end{equation*}$

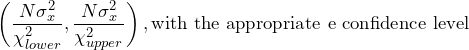
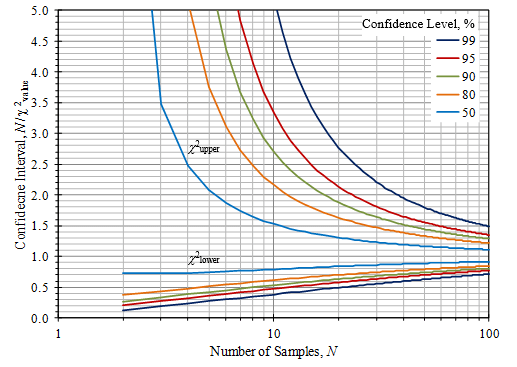
$Confidence intervals using the chi^2_{N} distribution for small sample size$

Figure 3.16. Confidence intervals using the $\chi^2_{N}$ distribution for small sample sizes.

For N > 100, we can use the normal distribution. The standard deviation of the variance estimate is √2/N σ_x², and we can use the (symmetrical) confidence intervals from Figure 3.13.