Mean Value
March 29, 2018
Back to: Random Testing
The mean value (μ) of a data set is the average or most probable value to occur. For many vibration signals, such as the one in Figure 3.1, the mean value is near zero because vibration occurs equally in positive and negative directions about a fixed position.
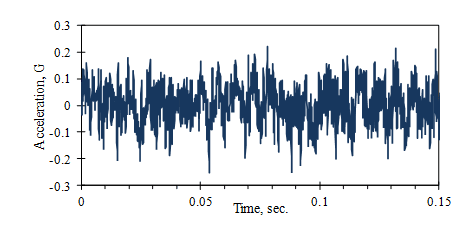
Figure 3.1. Random vibration signal (acceleration of car floor at 120 km/h).
Mean Value Equation
Equation 1 gives the mean value of a set of numbers, xn, n = 1, …, N.
(1) 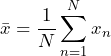
Equation 1
As previously mentioned, a vibration signal’s mean value usually cannot define the average amplitude because it is near zero. However, we can find the signal’s squared value and then compute its mean-square value.
Note also that a transducer’s electronics usually filter out the DC component of a vibration, which is the electrical equivalent of the mean value.
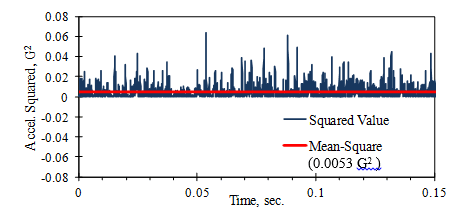
Mean-square Value
A signal’s mean-square value measures its average strength or “power.” Figure 3.2 includes the squared vibration signal from Figure 3.1 and its mean-square value.
Mean-square Equation
Equation 2 gives the mean-square value of a set of numbers, xn, n = 1, …, N.
(2) 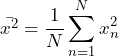
Equation 2
We can add the mean-square values when summing two signals with a mean value of 0. Consider the sum of two random variables, A and B. The square of (A+B) is (A+B)2 = A2 + 2 A·B + B2. If A and B are independent random variables with a zero mean value, then the value of (2 A·B) is zero. Therefore, the mean-square value of the sum is equal to the sum of the mean square values (given that the signals have a zero mean).