Variance

March 29, 2018

Variance (σ²) is the average of a data set’s squared difference from the mean. Equation 3 gives the variance of a set of numbers, x_n, n = 1, …, N, with a known mean value of μ.

(1) $\begin{equation*} \sigma^2=\frac{1}{N}\sum_{n=1}^{N}(x_{n}-\mu)^2 \end{equation*}$

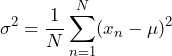
Equation 3

If the mean value is estimated from a set of numbers, then the variance is given by Equation 4.

(2) $\begin{equation*} \sigma^2=\frac{1}{N-1}\sum_{n=1}^{N}(x_{n}-\bar{x})^2 \end{equation*}$

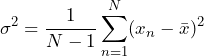
Equation 4

The value in the denominator before the summation is the number of independent values, or degrees of freedom, in the summation. X has been computed from the same set of numbers as Equation 4, so the value of the last term in the summation is predetermined. Therefore, the number of independent values in the summation is N – 1.

For a vibration signal with a mean value of zero, the variance is equal to the mean-square value. In general:

(3) $\begin{equation*} \sigma^2=\overline{x}^2-(\bar{x})^2 \end{equation*}$

Equation 5

When summing independent random variables, the variances are added, even with non-zero means.

The variance and standard deviation play an important role in determining the confidence interval—or, conversely, the uncertainty—of a statistical measurement. This topic is discussed further in the lesson on confidence intervals.