Skewness

March 29, 2018

Skewness measures a signal’s asymmetrical spread about its mean value. Equation 7 gives the skewness of a set of numbers, x_n, n = 1, …, N.

(1) $\begin{equation*} \gamma=\frac{1}{N\sigma^3}\sum_{n=1}^{N}(x_{n}-\mu)^3 \cong \frac{\frac{1}{N} \sum_{n=1}^{N} (x_{n}-\bar{x})^3}{(\frac{1}{N} \sum_{n=1}^{N} (x_{n}-\bar{x})^2)^{3/2}} \end{equation*}$

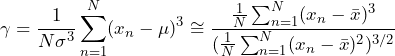
Equation 7

Skewness is the ratio of the average deviation from the mean cubed divided by the standard deviation cubed. It is dimensionless. For a random variable with normal distribution, the skewness is zero.

Figure 3.3 shows the turbulent pressure on the outside of the skin of an aircraft in flight. The pressure fluctuates more negatively than positively from the mean value, giving the skewness a value of γ = -0.32. The mean value is -0.03 kPa, and the standard deviation is 1.08 kPa.

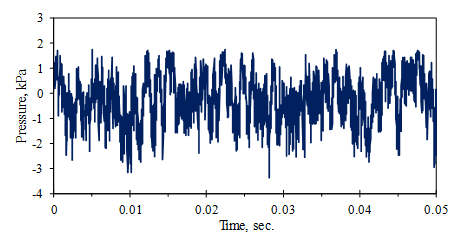
Turbulent pressure measured on the outside of the skin of an aircraft in flight

Figure 3.3. Turbulent pressure on the outside of the skin of an aircraft in flight.

The true mean value of the pressure (the atmospheric pressure, p_atm) has been removed from the signal electronically, so the measured signal is actually (p_–p_atm) and has a mean value near zero.