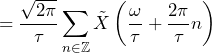DTFT of a Sampled Sequence

July 24, 2019

Sampling

Introduction to Sampling

Perfect Reconstruction from Samples

Examples of Waveform Sampling

Waveform Analysis Using Sampling

Distortion Introduced by Sampling

Frequency Domain Consequences of Sampling

Introduction

Definitions

DTFT of a Sampled Sequence

Fourier Transform of a Sampled Sequence

Sampling at the Nyquist Rate

Oversampling

Undersampling and Aliasing

Reconstruction Via Interpolation

Introduction to Interpolation

Waveform Approximation Using Lagrange Polynomial Interpolation

Perfect Waveform Reconstruction Using Sinc Interpolation

Interpolation in the Frequency Domain

Assistance from the Analog Components

Quantization noise and over-sampling

Quantization and Noise

Signal-to-Quantization Noise Ratio (SQNR)

Increasing SQNR by Increasing Bits Per Sample

Increasing SQNR by Increasing the Sample Rate

Differential Quantization / Delta Modulation

Differential Quantization and Delta Modulation

Noise Shaping / Delta-Sigma Modulation

Introduction

Delta-Sigma Encoding

Quiz: Sampling & Reconstruction

Back to: Sampling & Reconstruction

Suppose there is a signal x(t) with a Fourier transform of $\tilde{X}(\omega)$ . The signal is sampled every 𝜏 seconds, yielding the sequence y(n) = x(n𝜏). From the sampled sequence, a calculation yields the discrete-time Fourier transform (DTFT) $\tilde{Y}(\omega)$ of y(n).

Both a Fourier transform $\tilde{X}(\omega)$ and a DTFT $\tilde{Y}(\omega)$ have been identified. They come from two different transform definitions but originated from the same signal, x(t).

This prompts the question: do $\tilde{X}(\omega)$ and $\tilde{Y}(\omega)$ look anything alike? The answer is yes; in fact, $\tilde{Y}(\omega)$ looks like a scaled and repeated version of $\tilde{X}(\omega)$ . Below, Theorem 1 and Example 1 offer a more precise description as to why this is.

Theorem 1

Defining the DTFT of a sampled sequence in terms of the Fourier transform of the sampled waveform.

Let 𝗒(𝑛) ≜ 𝗑(𝑛𝜏) be the sample sequence of a waveform 𝗑(𝑡). 𝖥_s = 1/𝜏 is the sample rate. Let 𝖸̆(𝜔) be the DTFT of 𝗒(𝑛) and 𝖷̃ (𝜔) be the Fourier transform of 𝗑(𝑡). Then:

(1) $\begin{equation*} \tilde{Y}(\omega)=\sqrt{2\pi}F_{s}\sum_{n\in\mathbb{Z}}\tilde{X}(F_{s}[\omega-2\pi n]) \end{equation*}$

Proof

This theorem is difficult to prove without resorting to an “engineering hack” methodology such as multiplying the waveform by a train of impulse functions. However, the proof is manageable when we leverage the somewhat obscure yet powerful inverse Poisson summation formula (IPSF).

(2) $\begin{equation} \tilde{Y}(\omega)\triangleq\sum_{n\in\mathbb{Z}}y(n)e^{-i\omega n} \end{equation}$	by definition of DTFT
(3) $\begin{equation} =\sum_{n\in\mathbb{Z}}x(n\tau)e^{-i\omega n} \end{equation}$	by definition of y(n)
(4) $\begin{equation} =\sum_{n\in\mathbb{Z}}x(n\tau)e^{-i\frac{\omega}{\tau}n\tau} \end{equation}$	because τ/τ = 1
(5) $\begin{equation} =\frac{\sqrt{2\pi}}{\tau}\sum_{n\in\mathbb{Z}}\tilde{X}\left(\frac{\omega}{\tau}+\frac{2\pi}{\tau}n\right) \end{equation}$	by IPSF
(6) $\begin{equation} =\sqrt{2\pi}\text{F}_{s}\sum_{n\in\mathbb{Z}}\tilde{X}(\text{F}_{s}[\omega-2\pi n])\text{ by }\text{F}_{s}=1/\tau \end{equation}$	and absolute summability

The DTFT of the sample sequence is the Fourier transform of the original waveform. It is:

Repeated every 2𝜋 radians (in discrete world frequency, which is every 2 × 𝖥_s Hz in real-world frequency)
Dilated (made narrower) by a factor of 𝖥_s
Scaled (made taller) by a factor of √2𝜋𝖥_s

Figures 2.1-2.4 illustrate the extraction of the frequency content of a sampled waveform with a sample rate of Fs = 4 x fh.

Figure 2.1. Time waveform x(t).

Figure 2.2. Sample sequence.

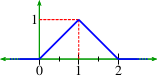
Figure 2.3. Fourier transform.

Figure 2.4. DTFT of y(n).

Examples 4 through 7 in this lesson and those that follow illustrate the importance of Theorem 1.

Frequency Content of a Sampled Waveform (Ex. 4)

F_s = 4 x f_h

Given the time waveform illustrated in Figure 2.1:

(7) $\begin{equation*} x(t)=\frac{1}{\sqrt2\pi}\left[\frac{sin(t/2)}{t/2}\right]^2 \triangleq \frac{1}{\sqrt2\pi}\text{sinc}^2\left(\frac{t}{2}\right) \end{equation*}$

The Fourier transform 𝖷̃ (𝜔) is the triangle function illustrated in Figure 2.3. The highest frequency component is 𝜔h = 1 radian/second or 𝖿h = 1/2𝜋 Hz. Therefore, the minimum sample rate is 𝖥s ≥ 2 × 𝖿h = 1/𝜋 and the maximum sample period is 𝜏 ≤ 𝖥_s = 𝜋.

The waveform 𝗑(𝑡) sampled at 𝖥_s ≜ 4 × 𝖿_h = 4 × 1/2𝜋 = 2/𝜋 (giving a sample period of 𝜏 = 1/𝖥_s = 𝜋/2) is illustrated in Figure 2.2.

With this sample rate and Theorem 1, the DTFT 𝖸̃(𝜔) of 𝗒(𝑛) is a repeated and scaled version of 𝖷̃ (𝜔). It is expressed as:

(8) $\begin{equation*} \tilde{Y}(\omega)=\sqrt{2\pi}F_{s}\sum_{n\in\mathbb{Z}}\tilde{X}(F_{s}[\omega-2\pi n]) \end{equation*}$

(9) $\begin{equation*} =\frac{2\sqrt{2\pi}}{\pi}\sum_{n\in\mathbb{Z}}\tilde{X}\left(\frac{2}{\pi}[\omega-2\pi n]\right) \end{equation*}$

Conclusion

𝖷̃ (𝜔) repeats every 2𝜋 (this is true of all DTFTs by definition)
𝖷̃ (𝜔) reaches zero when (2/𝜋) 𝜔 = 1 or 𝜔 = 𝜋/2; the higher the sample rate 𝖥_s, the narrower the triangle illustrated in Figure 2.3
The height of each triangle is 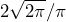$2\sqrt{2\pi}/\pi$ or about 1.596. The higher the sample rate 𝖥_s, the higher the triangle illustrated in Figure 2.3