Increasing SQNR by Increasing Bits Per Sample

December 3, 2019

Sampling

Introduction to Sampling

Perfect Reconstruction from Samples

Examples of Waveform Sampling

Waveform Analysis Using Sampling

Distortion Introduced by Sampling

Frequency Domain Consequences of Sampling

Introduction

Definitions

DTFT of a Sampled Sequence

Fourier Transform of a Sampled Sequence

Sampling at the Nyquist Rate

Oversampling

Undersampling and Aliasing

Reconstruction Via Interpolation

Introduction to Interpolation

Waveform Approximation Using Lagrange Polynomial Interpolation

Perfect Waveform Reconstruction Using Sinc Interpolation

Interpolation in the Frequency Domain

Assistance from the Analog Components

Quantization noise and over-sampling

Quantization and Noise

Signal-to-Quantization Noise Ratio (SQNR)

Increasing SQNR by Increasing Bits Per Sample

Increasing SQNR by Increasing the Sample Rate

Differential Quantization / Delta Modulation

Differential Quantization and Delta Modulation

Noise Shaping / Delta-Sigma Modulation

Introduction

Delta-Sigma Encoding

Quiz: Sampling & Reconstruction

Back to: Sampling & Reconstruction

Increasing the number of bits per sample will decrease the quantization noise and, therefore, increase SQNR. Theorem 3 quantifies this qualitative relationship for a full-scale sine waveform input. Take note that the SQNR increases approximately 6dB for every additional bit.

Theorem 3

Let SQNR be the signal to quantization noise ratio for a full-scale sinusoid input.

Let b be the number of bits used by a converter. Then:

(1) $\begin{equation*} \text{SQNR}=\frac{3}{2}(2^b-1)^2 \text{ for }b\geq0 \end{equation*}$

(2) $\begin{equation*} \text{SQNR}_{db}\triangleq10\text{log}_{10};\text{ SQNR}\approx[6.02b+1.76]\text{dB for }2^b>>1 \end{equation*}$

Proof

(1) The power P_s of a sine waveform Asin(2𝜋𝑓c 𝑡 + 𝜙) is A2/2

Proof: Let 𝜏 = 1/𝑓c be one period of the sine waveform.

(3) $\begin{equation*} P_{s}\triangleq\frac{1}{\tau}\int_{0}^{\tau}[A\text{sin}(2\pi fct+\phi)]^2\text{d}t \end{equation*}$

(4) $\begin{equation*} =\frac{\text{A}^2}{2}\int_{0}^{\tau}\text{sin}2(2\pi fct+\phi)\text{d}t \end{equation*}$

(5) $\begin{equation} =\frac{\text{A}^2}{2\tau}\int_{0}^{\tau}[1-\text{cos}(4\pi fct+2\phi)]\text{d}t \end{equation}$	by half-angle formula/squared identity
(6) $\begin{equation} =\frac{\text{A}^2}{2\tau}\int_{0}^{\tau}1\text{d}t-\int_{0}^{\tau}\text{cos}(4\pi fct+2\phi)]\text{d}t \end{equation}$	by half-angle formula/squared identity

(7) $\begin{equation*} =\frac{\text{A}^2}{2} \end{equation*}$

(2) For SQNR:

(8) $\begin{equation} \text{SQNR}\triangleq\frac{\text{P}_{s}}{\text{P}_{n}} \end{equation}$	by definition of SQNR
(9) $\begin{equation} =\frac{\text{A}^2/2}{\Delta^{2}12} \end{equation}$	by item (1) above and the proposition Var v(n)
(10) $\begin{equation} =\frac{\Delta2}{12} \end{equation}$	from the lesson Quantization and Noise
(11) $\begin{equation} =[(2^{\text{b}-1}-1/2)\Delta]^2/2\times\Delta^2/12 \end{equation}$	from the lesson Quantization and Noise

(12) $\begin{equation*} =6(2^{\text{b}-1}-1/2)^2=6(1/2\times2^{\text{b}}-1/2)^2=\frac{6}{4}(2^{\text{b}}-1)^2=\frac{3}{2}(2^{\text{b}}-1)^2 \end{equation*}$

(3) For SQNRdB:

(13) $\begin{equation} \text{SQNR}_{dB}\triangleq10\log_{10}\text{SQNR} \end{equation}$	by the definition of SQNR_dB
(14) $\begin{equation} =10\log_{10}[6(2^{\text{b}-1}-1/2)^2] \end{equation}$	by proof (2)
(15) $\begin{equation} =10\log_{10}6+10\log_{10}[(2^{\text{b}-1}-1/2)^2] \end{equation}$	by property of logarithms
(16) $\begin{equation} 10\log_{10}6+20\log_{10}(2^{\text{b}-1}-1/2) \end{equation}$	by property of logarithms
(17) $\begin{equation} =10\log_{10}6+20\log_{10}[1/2(2^{\text{b}}-1)] \end{equation}$
(18) $\begin{equation} =10\log_{10}6+20\log_{10}1/2+20\log_{10}(2^{\text{b}}-1) \end{equation}$	by property of logarithms
(19) $\begin{equation} =10\log_{10}6+10\log_{10}(1/2)^2+20\log_{10}(2^{\text{b}}-1) \end{equation}$	by property of logarithms
(20) $\begin{equation} =20\log_{10}(2^{\text{b}}-1)+10\log_{10}6/4 \end{equation}$	by property of logarithms
(21) $\begin{equation} \approx 20\log_{10}(2^{\text{b}})+10\log_{10}3/2 \end{equation}$	for 2^b>>1
(22) $\begin{equation} =20[\log_{10}2]\text{b}+10\log_{10}3/2 \end{equation}$	by property of logarithms
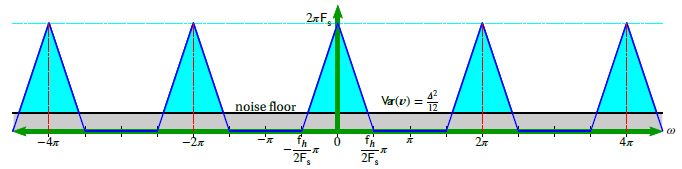
(23) $\begin{equation} \approx 6.02\text{b}+1.76 \end{equation}$

Over-Sampling with Quantization Uniformly Distributed White Noise

Theorem 3 is a theoretical ideal. In practice, an N-bit converter has issues with inherent noise and doesn’t provide N bits of precision. Given this, system engineers want to know how many effective bits they can achieve. The b in Theorem 3 is equated in terms of SQNRdB to yield the following quantity called ENOB.

Let SINAD be the signal-to-noise-and-distortion ratio. Then:

(24) $\begin{equation*} \text{ENOB}\triangleq[\text{SNIAD}-1.76]/6.02 \end{equation*}$

(13) $\begin{equation} \text{SQNR}_{dB}\triangleq10\log_{10}\text{SQNR} \end{equation}$	by the definition of SQNR_dB
(14) $\begin{equation} =10\log_{10}[6(2^{\text{b}-1}-1/2)^2] \end{equation}$	by proof (2)
(15) $\begin{equation} =10\log_{10}6+10\log_{10}[(2^{\text{b}-1}-1/2)^2] \end{equation}$	by property of logarithms
(16) $\begin{equation} 10\log_{10}6+20\log_{10}(2^{\text{b}-1}-1/2) \end{equation}$	by property of logarithms
(17) $\begin{equation} =10\log_{10}6+20\log_{10}[1/2(2^{\text{b}}-1)] \end{equation}$
(18) $\begin{equation} =10\log_{10}6+20\log_{10}1/2+20\log_{10}(2^{\text{b}}-1) \end{equation}$	by property of logarithms
(19) $\begin{equation} =10\log_{10}6+10\log_{10}(1/2)^2+20\log_{10}(2^{\text{b}}-1) \end{equation}$	by property of logarithms
(20) $\begin{equation} =20\log_{10}(2^{\text{b}}-1)+10\log_{10}6/4 \end{equation}$	by property of logarithms
(21) $\begin{equation} \approx 20\log_{10}(2^{\text{b}})+10\log_{10}3/2 \end{equation}$	for 2^b>>1
(22) $\begin{equation} =20[\log_{10}2]\text{b}+10\log_{10}3/2 \end{equation}$	by property of logarithms
(23) $\begin{equation} \approx 6.02\text{b}+1.76 \end{equation}$