Increasing SQNR by Increasing the Sample Rate

February 3, 2020

The lesson Quantization and Noise proves that the quantization noise floor is flat with a power of 𝛥2/12 for all 𝜔. However, the band-limited signal 𝖸̃(𝜔) is not. Moreover, 𝖸̃(𝜔) gets “taller” and effectively more narrow as 𝖥s increases (see Theorem 1 in the lesson DTFT of a Sampled Sequence.)

Therefore, the signal-to-noise ratio drops as 𝖥s increases as long as there is proper low-pass reconstruction filtering at the output. This means that more of the quantization noise is filtered out. We refer again to the figure presented in the lesson Increasing SQNR by Increasing Bits Per Sample.

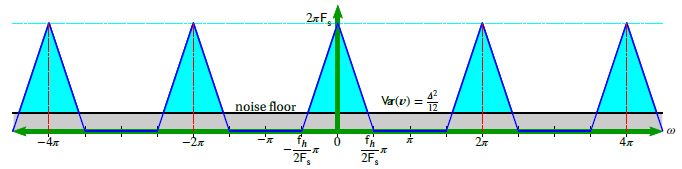
the noise floor increases as the number of bits decreases

In the figure, the noise floor increases as the number of bits decreases (𝛥 will increase) but the noise floor does not increase with the sample rate.

Thus, with a sufficiently high sample rate (𝖥s) and sufficient low-pass filtering, it is possible to design a system with a high SNQR even with just one bit (𝑏 = 1). More specifically, every time the sample rate is doubled, the SQNR increases by a factor of 4 (about 6dB or 1 bit). This is demonstrated by the next theorem.

Theorem 4

Proof

(1) $\begin{equation*} P'_{s}\triangleq\int_{\omega\in\mathbb{R}}[2x(2\omega)]^2d\omega \end{equation*}$

(2) $\begin{equation*} =4\int_{\omega\in\mathbb{R}}x^2(2\omega)d\omega \end{equation*}$

(3) $\begin{equation*} =4\int_{\omega\in\mathbb{R}}x^2(v)(1/2)dv\text{ where }v\triangleq2\omega\implies d\omega=(1/2)dv \end{equation*}$

(4) $\begin{equation*} =2P_{s} \end{equation*}$

As a low-pass filter eliminates half the spectral content:

(5) $\begin{equation*} P'\triangleq(1/2P)P_{n} \end{equation*}$

(6) $\begin{equation*} \text{SQNR}'\triangleq(P'_{s}/P'_{n})=\left[\frac{2P}{(1/2)P_{n}}\right]=4(P_{s}/P_{n})\triangleq 4\text{SQNR} \end{equation*}$

(7) $\begin{equation*} \text{SQNR}_{dB}\triangleq 10\text{log}_{10}\text{SQNR}' \end{equation*}$

(8) $\begin{equation*} =10\text{log}_{10}[4\text{SQNR}]=10\text{log}_{10}(4)+10\text{log}_{10}(\text{SQNR}) \end{equation*}$

(9) $\begin{equation*} \approx\text{SQNR}_{dB}+6.02 \end{equation*}$

Example

Suppose we want to sample at 𝑏 = 1 bit.

According to Theorem 3, 𝖲𝖰𝖭𝖱_𝖽𝖡 ≈ 6.02 × 1 + 1.76 = 7.78 dB. In an ideal system, the 𝖲𝖰𝖭𝖱_𝖽𝖡 for 𝑏 = 16 bits is 𝖲𝖰𝖭𝖱_𝖽𝖡 ≈ 6.02 × 16 + 1.76 ≈ 98 dB.

To sample at 𝑏 = 1 and have a quality of 𝑏 = 16 (98dB), how fast do we need to sample?

According to Theorem 4, SQNR increases by 6.02dB every time the sample rate doubles. Therefore, the sample rate must double (98 − 7.78)/6.02 = 14.99 = 15 times. In other words, the sample rate must increase to 215 or 32,768 times the Nyquist rate.

Therefore, if our original sample rate was 44.1 kHz, our new sample rate would need to be approximately 1.45 GHz.

Alternative Techniques

A high sample rate tends to be impractical and sometimes undesirable. However, there are alternative techniques with more relaxed sample rates. These techniques include:

Differential quantization/delta modulation encodes the difference between two successive samples rather than encoding every sample as-is. If the consecutive samples are correlated⁠—as we might expect for band-limited signals⁠—the difference between the samples tends to be small and results in less quantization noise. The next lesson discusses delta modulation in more detail.
Noise shaping is often implemented using a signal processing topology called delta-sigma modulation. This topology uses a feedback path that passes the desired signal through and pushes the noise energy into higher frequency bands (noise shaping) which can subsequently be filtered out. Thus, SQNR is reduced, but the quantization is only 1-bit and the sample rate may only need to be increased by 256 times the Nyquist rate. Noise shaping and delta-sigma modulation are presented in the Noise Shaping/Delta-Sigma Modulation section.