Differential Quantization and Delta Modulation
February 7, 2020
Back to: Sampling & Reconstruction
In previous lessons, we established that we can increase the signal-to-quantization noise ratio (SQNR) by increasing the number of bits per sample or increasing the sample rate. A third method involves changing the modulation technique.
Pulse Code Modulation
In earlier lessons, the math assumed that sampling was performed using the pulse code modulation (PCM) technique. PCM quantizes the signal waveform 𝗑(𝑡) every sample period (𝜏) and yields the sample sequence 𝗒(𝑛) ≜ 𝖰[𝗑(𝑛𝜏)].
Although it is widely used, PCM disregards the fact that band-limited waveforms cannot change quickly at high sample rates. If they did, they would have high-frequency content and would not be band-limited.
Differential Quantization
Band-limited signals cannot change quickly, so the difference between consecutive samples should be relatively small. Therefore, the difference between consecutive samples 𝗑(𝑛) − 𝗑(𝑛 − 1) should be quantized rather than quantizing each raw sample 𝗑(𝑛).
Sampling by quantizing the difference is called differential quantization. Differential quantization requires fewer bits for an equivalent SQNR value.
So far, this description is based on qualitative and intuitive grounds. For quantitative analysis, the variance of the difference between two consecutive samples should be sampled and then compared to the variance of PCM-based sampling.
Selecting a Method
The following proposition shows that the best method depends on how correlated the signal is. If the signal is highly correlated, as might be expected with a high sample rate relative to the bandwidth, then the differential approach tends to yield a lower variance (less distortion). If the signal is not highly correlated, as might be expected with a low sample rate, then the PCM approach tends to yield less distortion.
Proposition
- Let Rxx(m) be the auto-correlation of x(n),
- Yxx (m) ≜ [ Rxx (m)] / (𝜎x ) 2 be the auto-covariance of x(n),
- (𝜎x ) 2 be variance of x(n), and
- (𝜎d ) 2 be the variance of x(n) – x(n-1) (using differential quantization).
Then:
(1) ![]()
Proof
|
(2) |
by definition of variance σ2 |
|
(3) |
by the binomial theorem |
|
(4) |
by the wide-sense stationary property |
|
(5) |
by definition of variance σ2 |
|
(6) |
by the definition of Rxx(m) |
|
(7) |
by the definition of yxx(m) |
|
(8) |
by the definition of yxx(m) |
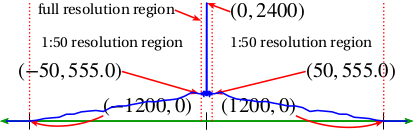
Small Correlation
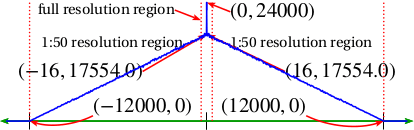
Large Correlation
According to the proposition above, if yxx (1) > 1/2, then the differential encoding introduces less distortion.
