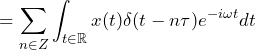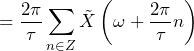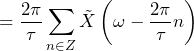Fourier Transform of a Sampled Sequence

July 29, 2019

According to Theorem 1, 𝖸̃(𝜔) is the discrete-time Fourier transform of the sample sequence 𝗒(𝑛). What is the Fourier transform of that sample sequence?

First, let’s note that the Fourier transform is defined for functions over ℝ or ℂ (real or complex). It is not defined for sequences, which are functions over the set of integers ℤ.

However, in an attempt to compute such a transform, it is possible to use the infinity enabled Dirac delta 𝛿(𝑡) to define a comb function 𝗑𝑑 (𝑡) as:

(1) $\begin{equation*} x_{d}(t)=\sum_{n\in\mathbb{Z}}x(n\tau)\delta(t-n\tau) \end{equation*}$

Mathematical Definition

Ignoring that real-world ADCs/DACs cannot implement infinite voltage handling, the following equations lead to the mathematical definition of the sampled sequence’s Fourier transform. The result is similar in form to the DTFT in Theorem 1.

(2) $\begin{equation} \tilde{Y}(\omega)=\int_{t\in\mathbb{R}}\text{x}_{d}(t)e^{-i\omega t}dt \end{equation}$	by definition of FT
(3) $\begin{equation} =\int_{t\in\mathbb{R}}\left[\sum_{n\in Z}x(t)\delta(t-n\tau)\right]e^{-i\omega t}dt \end{equation}$	by definition of x_d(t)
(4) $\begin{equation} =\sum_{n\in Z}\int_{t\in\mathbb{R}}x(t)\delta(t-n\tau)e^{-i\omega t}dt \end{equation}$	by linearity of integral over t of dt
(5) $\begin{equation} =\sum_{n\in Z}x(n\tau)e^{-i\omega n\tau} \end{equation}$	by definition of δ(t)
(6) $\begin{equation} =\frac{2\pi}{\tau}\sum_{n\in Z}\tilde{X}\left(\omega+\frac{2\pi}{\tau}n\right) \end{equation}$	by IPSF
(7) $\begin{equation} =\frac{2\pi}{\tau}\sum_{n\in Z}\tilde{X}\left(\omega-\frac{2\pi}{\tau}n\right) \end{equation}$	by absolute summability property
(8) $\begin{equation} =2\pi \text{F}_{s}\sum_{n\in Z}\tilde{X}(\omega-2\pi \text{F}_{s}n) \end{equation}$	by definition of sample rate F_s

Conclusion

𝖷̃ (𝜔) repeats every 𝜔 = 2𝜋𝖥s radians/second, or every 𝖥s Hertz
𝖷̃ (𝜔) reaches 0 at 𝜔 = 1 just as it did pre-sampling (sample rate 𝖥s does not affect the width of the triangle)
The height of each triangle is 2𝜋𝖥s; the higher the sample rate 𝖥s, the taller the triangle