CoursesCertificatesBack to VR.com

MENU

Sampling at the Nyquist Rate

August 1, 2019

Sampling

Introduction to Sampling
Perfect Reconstruction from Samples
Examples of Waveform Sampling
Waveform Analysis Using Sampling
Distortion Introduced by Sampling

Frequency Domain Consequences of Sampling

Introduction
Definitions
DTFT of a Sampled Sequence
Fourier Transform of a Sampled Sequence
Sampling at the Nyquist Rate
Oversampling
Undersampling and Aliasing

Reconstruction Via Interpolation

Introduction to Interpolation
Waveform Approximation Using Lagrange Polynomial Interpolation
Perfect Waveform Reconstruction Using Sinc Interpolation
Interpolation in the Frequency Domain
Assistance from the Analog Components

Quantization noise and over-sampling

Quantization and Noise
Signal-to-Quantization Noise Ratio (SQNR)
Increasing SQNR by Increasing Bits Per Sample
Increasing SQNR by Increasing the Sample Rate

Differential Quantization / Delta Modulation

Differential Quantization and Delta Modulation

Noise Shaping / Delta-Sigma Modulation

Introduction
Delta-Sigma Encoding
Quiz: Sampling & Reconstruction

Back to: Sampling & Reconstruction

In Example 1, the time waveform x(t) was sampled at π–₯s = 4 Γ— 𝖿h. The resulting DTFT spectral images were spread out in the DTFT frequency domain.

By examining these results, it is apparent that the minimum sample rate is π–₯s = 2 Γ— 𝖿h. Anything less would result in the overlap of spectral images.

The π–₯s = 2Β  Γ— 𝖿h rate is called the Nyquist rate. Example 5 is similar to Example 4, but the sample rate π–₯s is reduced to the Nyquist rate.

Frequency Content of a Waveform Sampled at Nyquist Rate (Ex. 5)

Given the time waveform illustrated in Figure 2.1:

(1)   \begin{equation*} x(t)=\frac{1}{\sqrt{2\pi}}\left[\frac{\sin(t/2)}{t/2}\right]^2 \triangleq \frac{1}{\sqrt{2\pi}}sinc^2\left(\frac{t}{2}\right) \end{equation*}

The Fourier transform 𝖷̃(πœ”) is the triangle function illustrated in Figure 2.3 with the highest frequency component of 𝖿h = 1/2πœ‹ Hz.

The waveform x(t) sampled at π–₯s β‰œ 2 Γ— 𝖿h = 4 Γ— 1/2πœ‹ = 1/πœ‹ gives a sample period of 𝜏 = 1/π–₯s = πœ‹ and is illustrated in Figure 2.5.

Sample sequence

Figure 2.5. Sample sequence.

Using this sample rate and Theorem 1, a DTFT 𝖸̃(πœ”) of y(n) is expressed as:

(2)   \begin{equation*} \tilde{Y}(\omega)=\sqrt{2\pi}F_{s}\sum_{n\in\mathbb{Z}}\tilde{X}(F_{s}[\omega-2\pi n]) \end{equation*}

(3)   \begin{equation*} =\frac{\sqrt{2\pi}}{\pi}\sum_{n\in\mathbb{Z}}\tilde{X}\left(\frac{1}{\pi}[\omega-2\pi n]\right) \end{equation*}

Conclusion

  • 𝖷̃(πœ”) repeats every 2πœ‹ (this is true of all DTFTs)
  • 𝖷̃(πœ”) reaches 0 when (1/πœ‹) πœ” = 1 or πœ” = πœ‹
  • The height of each triangle is 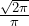\frac{\sqrt{2\pi}}{\pi} or about 0.798 (see Figures 2.6 and 2.7)
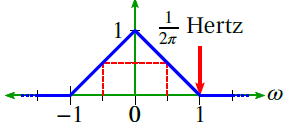
Fourier transform

Figure 2.6. Fourier transform.

DTFT

Figure 2.7. DTFT.