Perfect Waveform Reconstruction Using Sinc Interpolation
September 6, 2019
Back to: Sampling & Reconstruction
The previous waveform approximation method demonstrates that we can achieve a close approximation by increasing the sample rate towards infinity. This is an important result of the mathematical field of functional analysis.
However, digital systems don’t sample at an infinite rate or even close to it. Thus, the goal is to sample at a reasonable rate and still perfectly reconstruct/synthesize the original waveform.
“Is synthesis possible?” The answer is yes. This is one of the most surprising results in mathematics and one of the most fundamental results in DSP. According to the sampling theorem, if a sample rate is at least two times the highest frequency component of the sampled waveform, then perfect reconstruction is possible.
Theorem 2
The Sampling Theorem
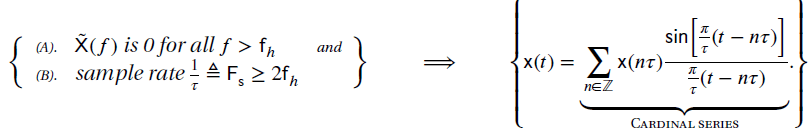
Mathematically, the sampling theorem states that a sequence of sinc functions (called a “cardinal series”) is a basis for a band-limited function 𝗑(𝑡) …, and the coefficients for the projection of 𝗑(𝑡) onto the basis are the samples 𝗑(𝑛𝜏) of 𝗑(𝑡).
As we saw in the previous lesson, polynomial interpolation between samples results in an approximation of the original cosine waveform. Sinc interpolation, on the other hand, results in perfect reconstruction. See the graphs below.
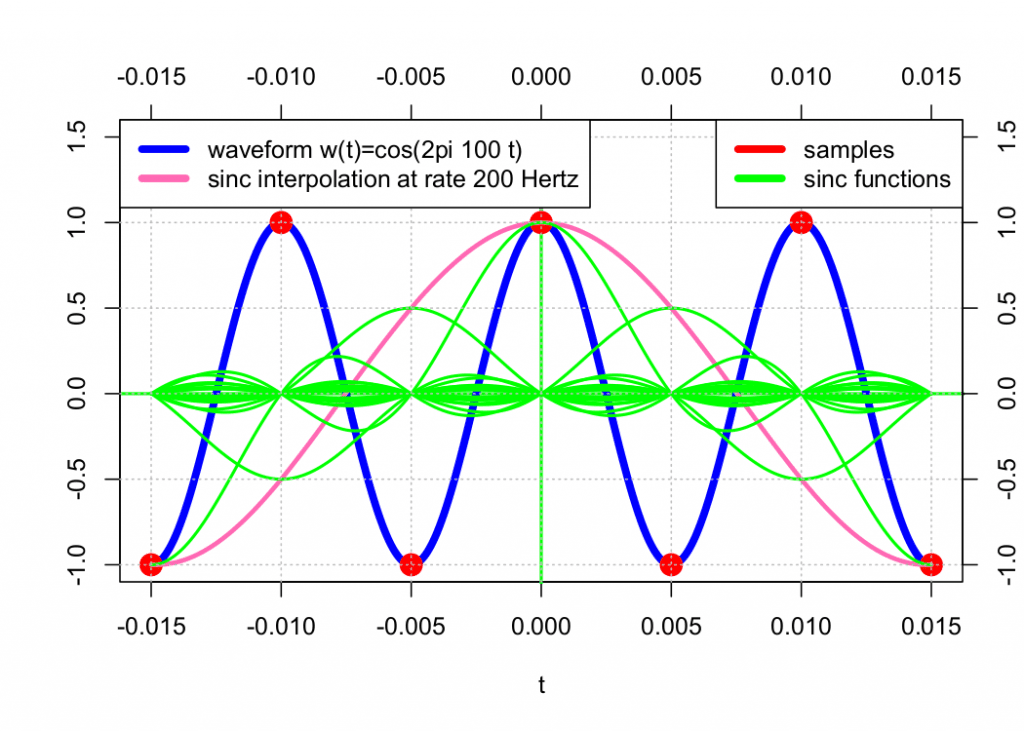
2 x F(s)
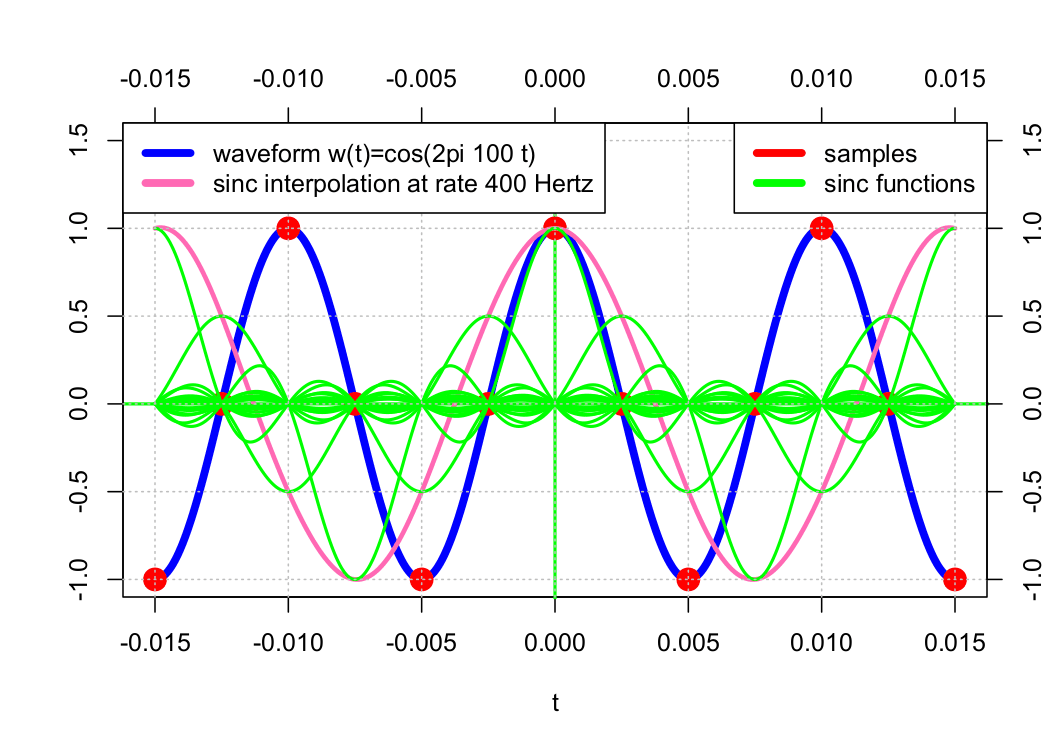
4 x F(s)
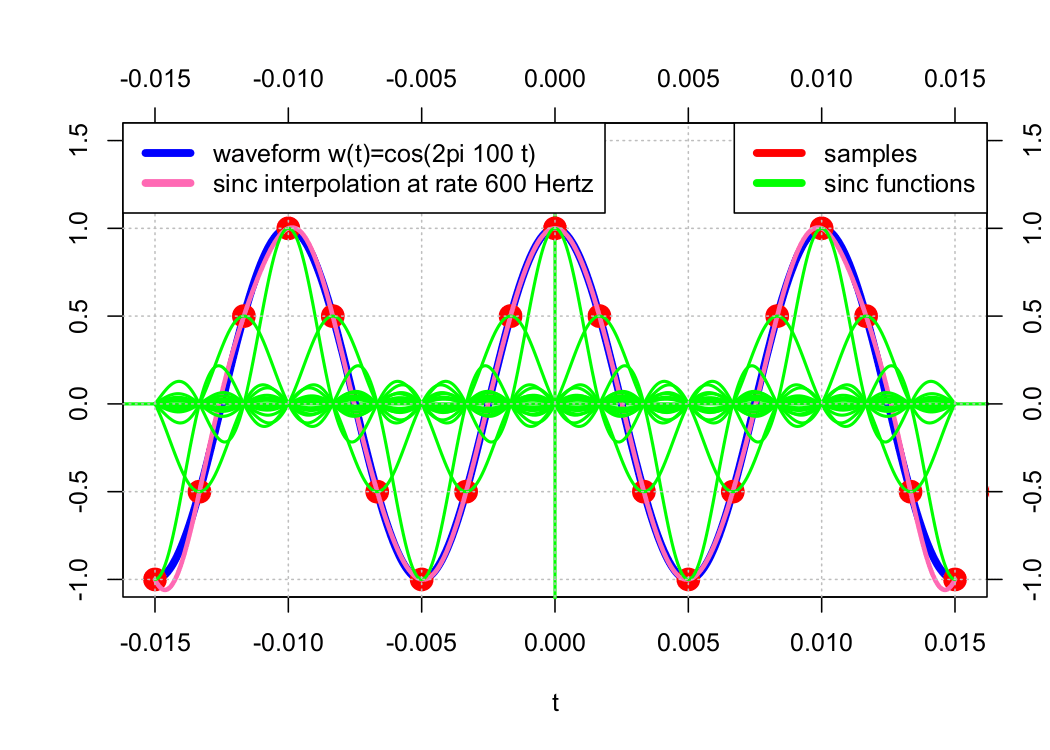
6 x F(s)
