Waveform Approximation Using Lagrange Polynomial Interpolation

Back to: Sampling & Reconstruction

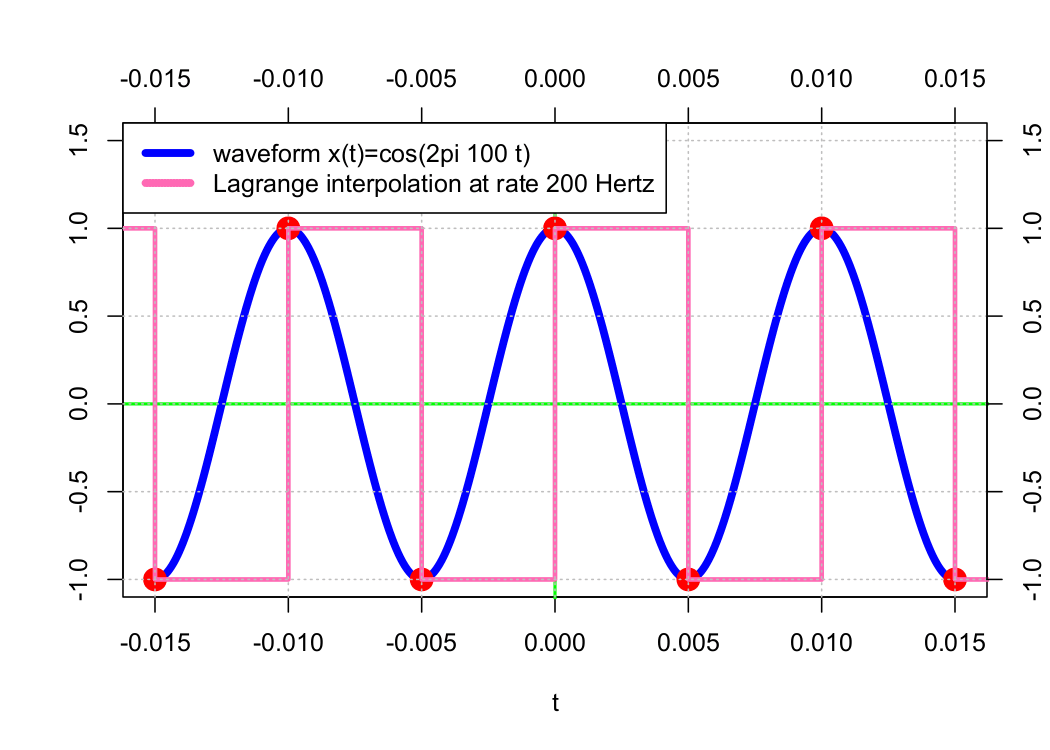
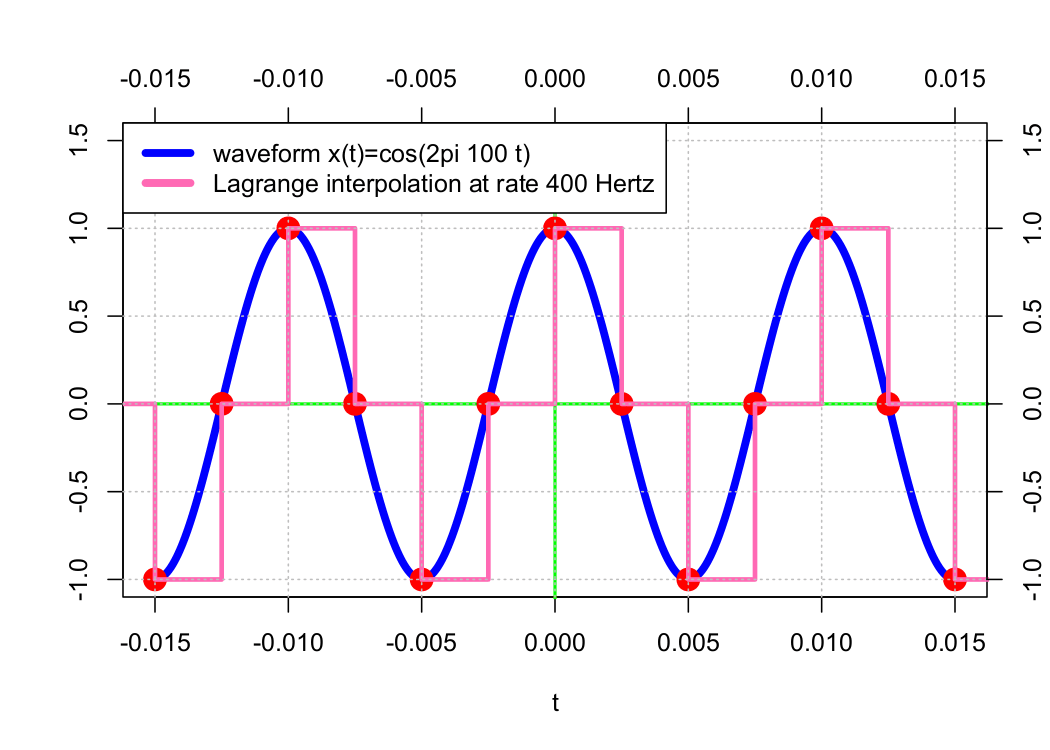
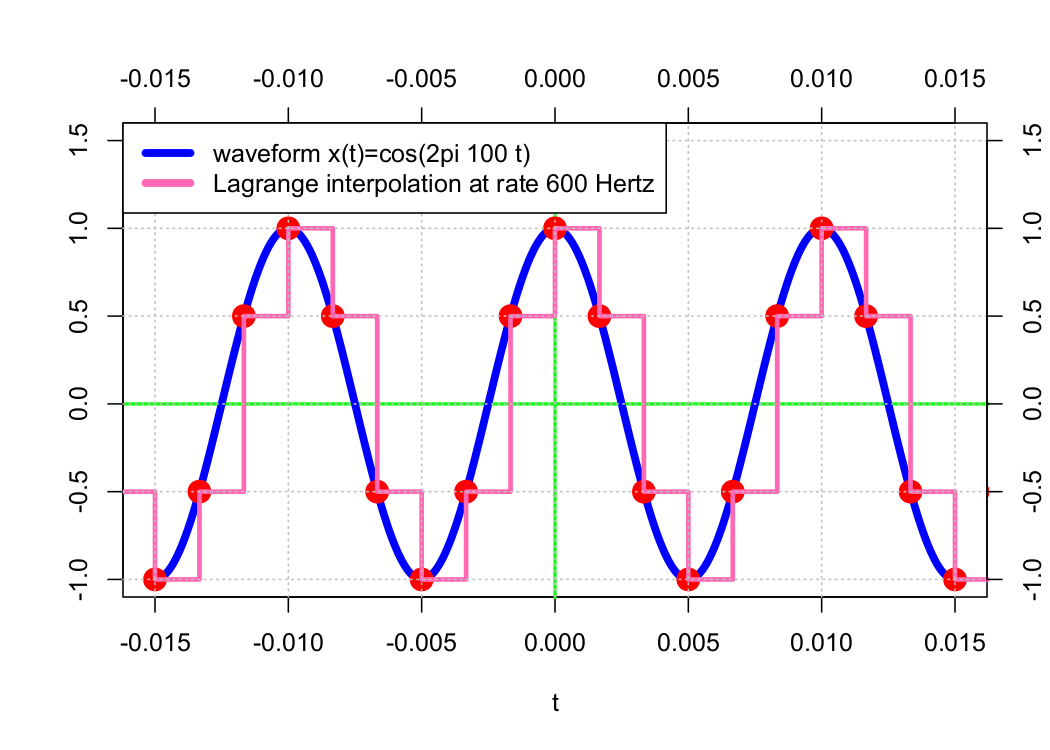
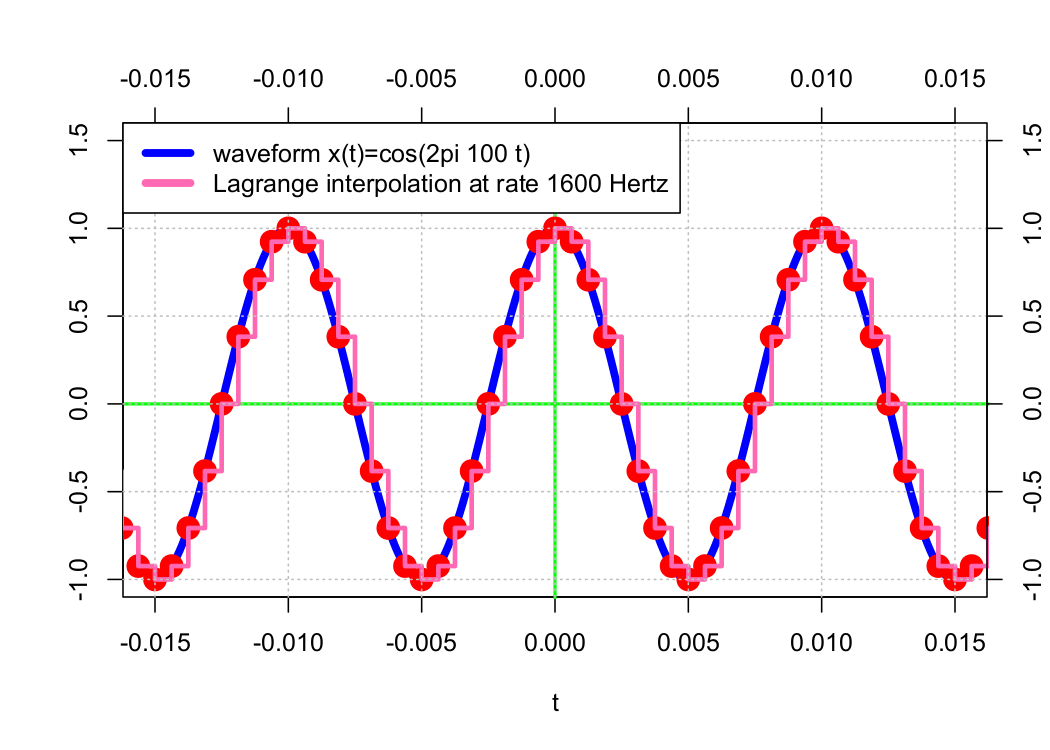
Reconstructing a waveform 𝗑(𝑡) from its samples 𝗑(𝑛𝜏) requires some form of interpolation. One of an infinite number of possible methods is Lagrange interpolation, which connects n points using an order-n − 1 polynomial. Examples of this method are presented below.

Order-0 (Stair-Step) Polynomial Interpolation

Order-1 (Line) Polynomial Interpolation

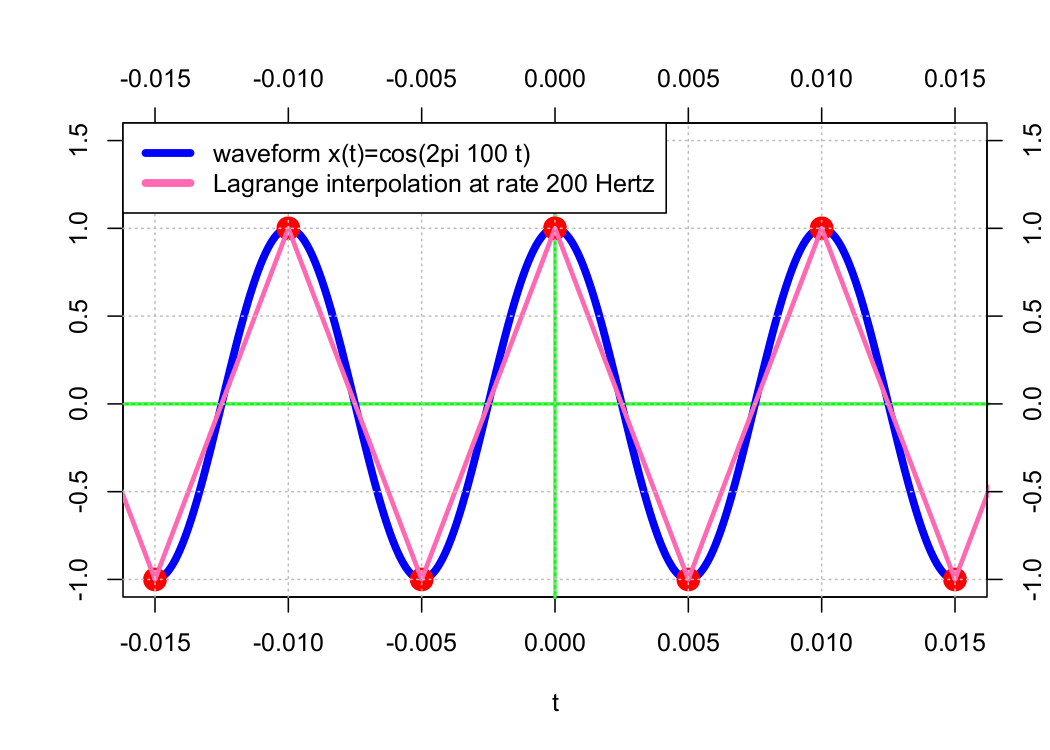
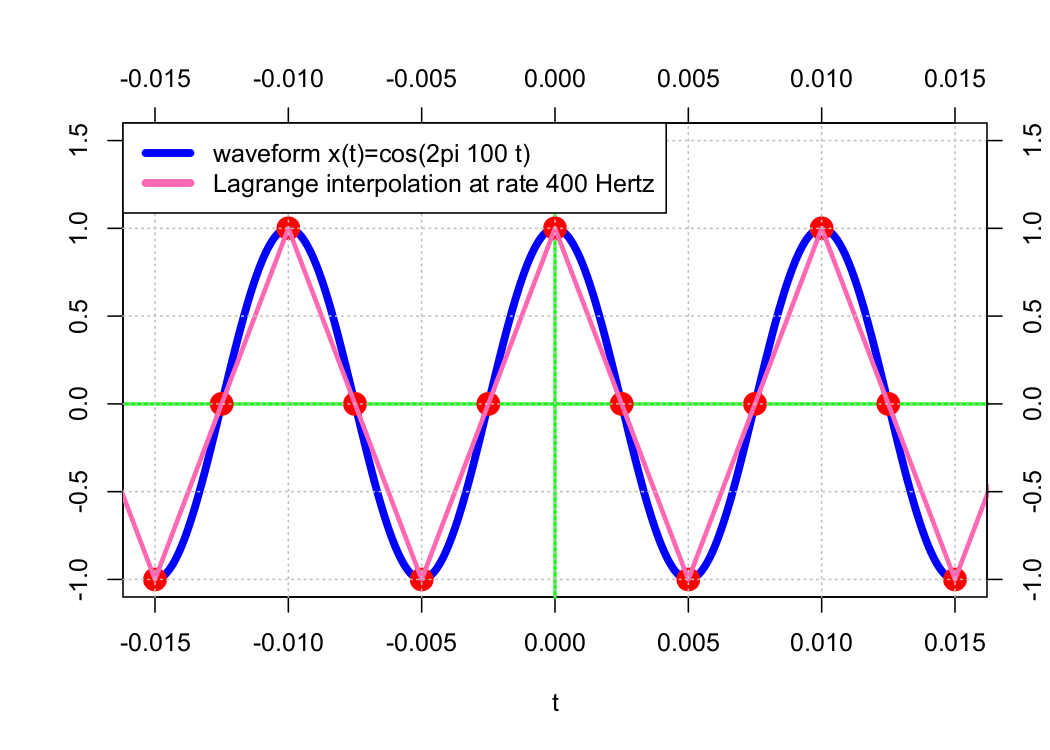
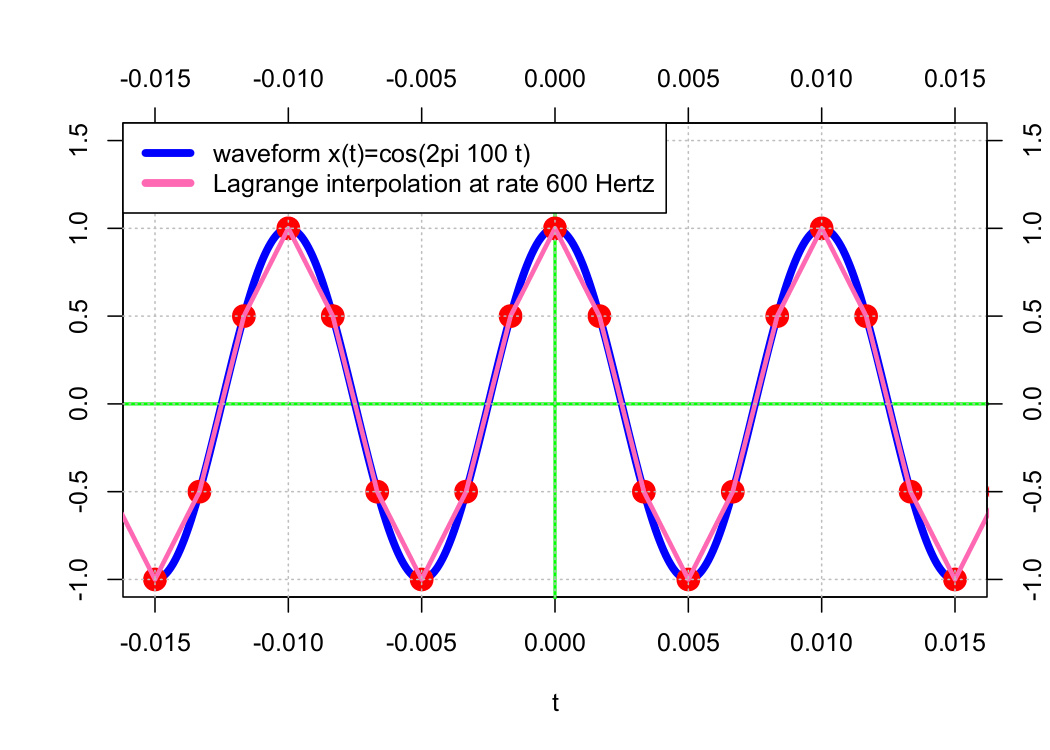
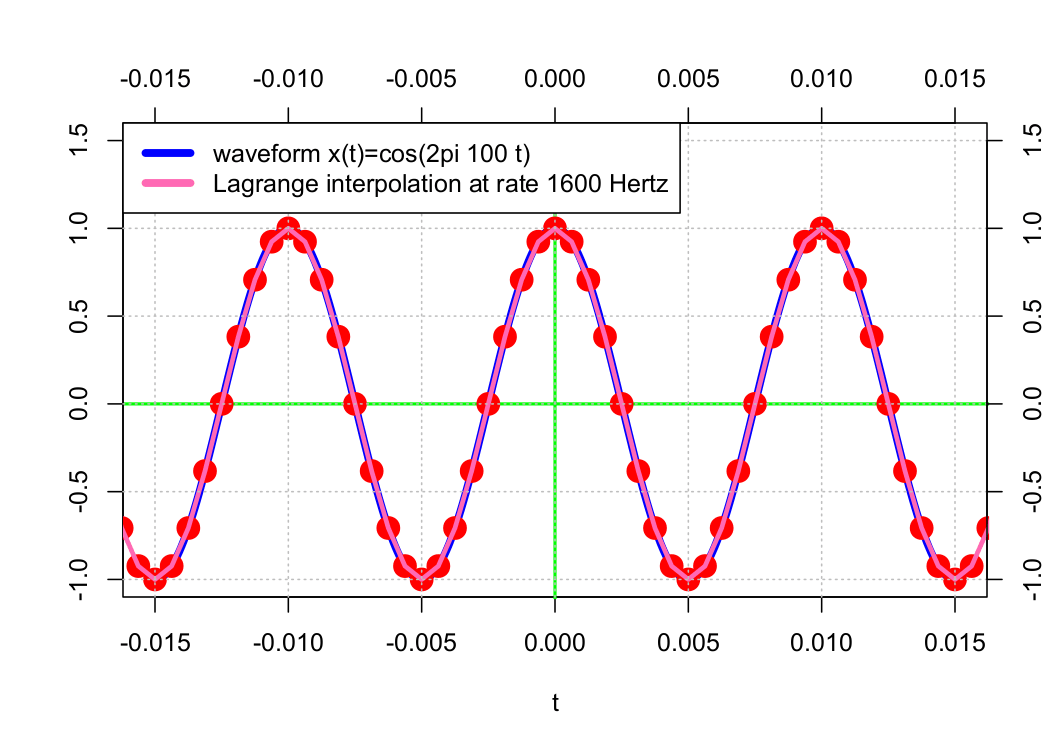
In the examples above, the approximation waveform appears to get “closer” to the original waveform as the sample rate increases. As a result of B-splines, the original waveform can be precisely approximated by increasing the sample rate toward infinity.

Particularly, the order-0 interpolation is equivalent to interpolation using the order-0 B-spline N0(t) and the order-1 interpolation using the order-0 B-spline N1(t). The sequence of shifted B-splines (𝖭0(𝑡 − 𝑛𝜏)) forms an orthonormal basis, and for any 𝑚 ≥ 1, the set of shifted B-splines (𝖭m(𝑡 − 𝑛𝜏)) forms a Riesz basis (but not an orthonormal basis).