Windowing
June 2, 2021
Process Data
Analyze Data
System Identification
Mathematical Foundations
Back to: Fundamentals of Signal Processing
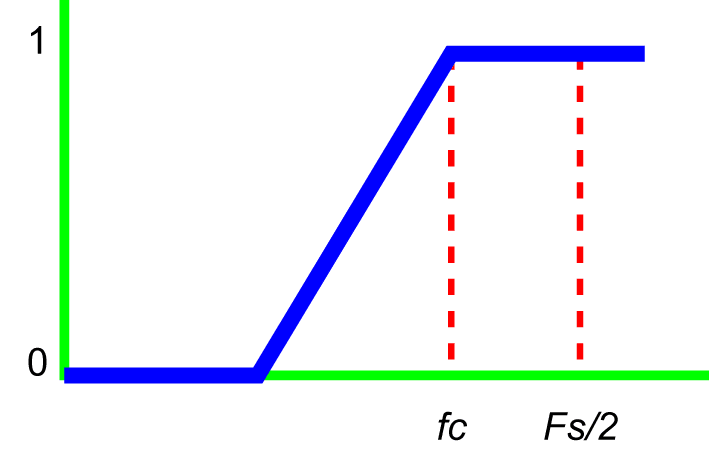
Illustration of a high-pass filter.
In the previous lessons, we discussed filtering—an operation that removes user-defined frequency components from a time or frequency signal to improve signal clarity.
Engineers can apply filters directly in the time domain, but filtering data in the frequency domain requires a transform to move the data from time to frequency, such as the fast Fourier transform (FFT).
Windowing Signals
Engineers may apply a window function to a time-domain signal before transforming the data with the FFT. Windowing is often necessary because the FFT assumes the time-domain signal is periodic—i.e., the data sample repeats seamlessly at its boundaries. Real-world vibration is usually random, so a data sample will not likely start and end at the same phase and amplitude levels.
Without a window function, the signal generated from the data sample will likely have discontinuities, which generate spurious amplitudes in the adjacent frequencies called leakage. Windowing mitigates spectral leakage by tapering the signal at its boundaries before performing the FFT.
Window Functions
A window sequence is similar in structure to a finite impulse response (FIR) filter but differs in application. A window sequence is applied by multiplying it with a data sequence (windowing the data), whereas an FIR filter is applied by convolving it with a data sequence (filtering the data).
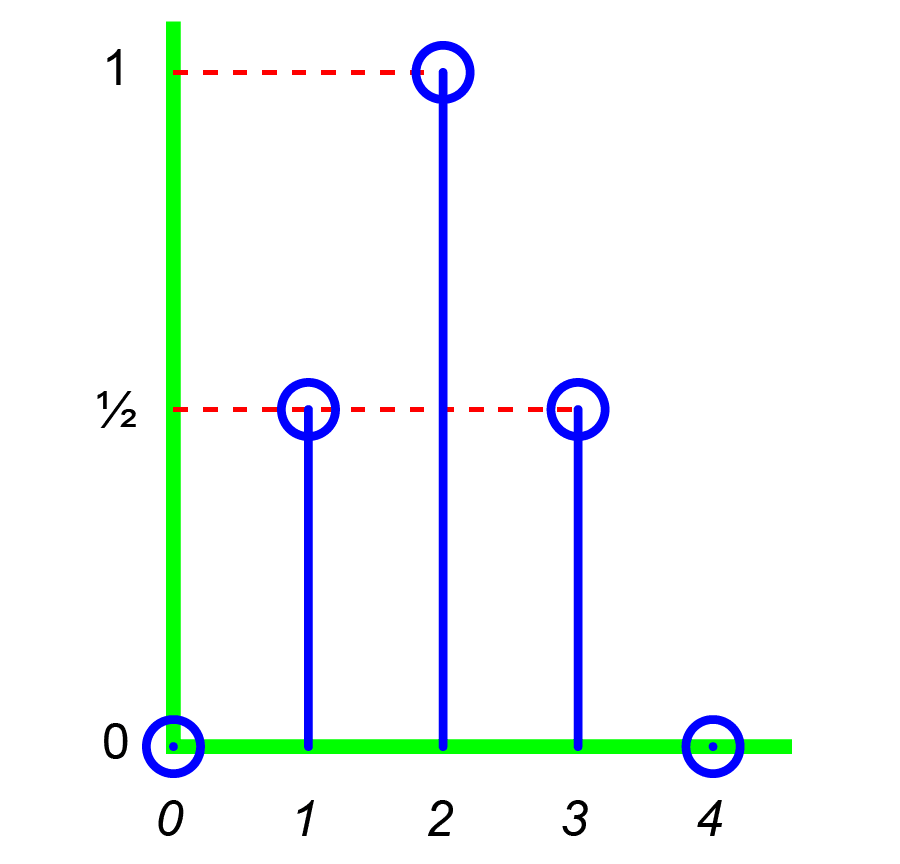
Window sequence
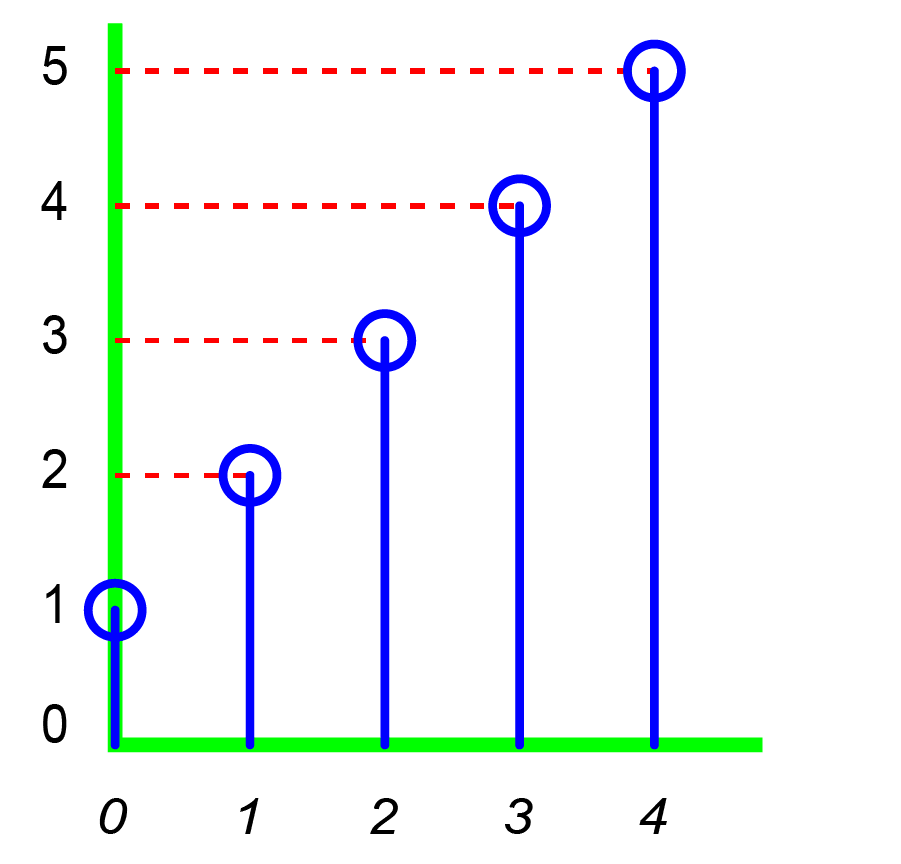
Data sequence
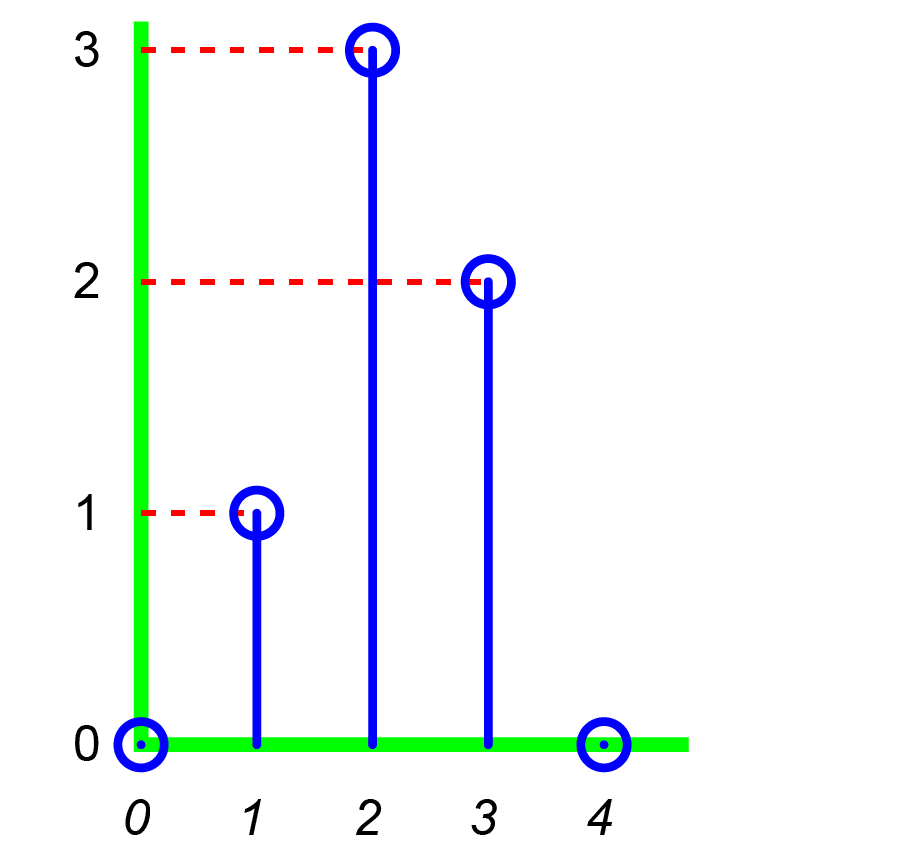
Window times data (“windowing”)
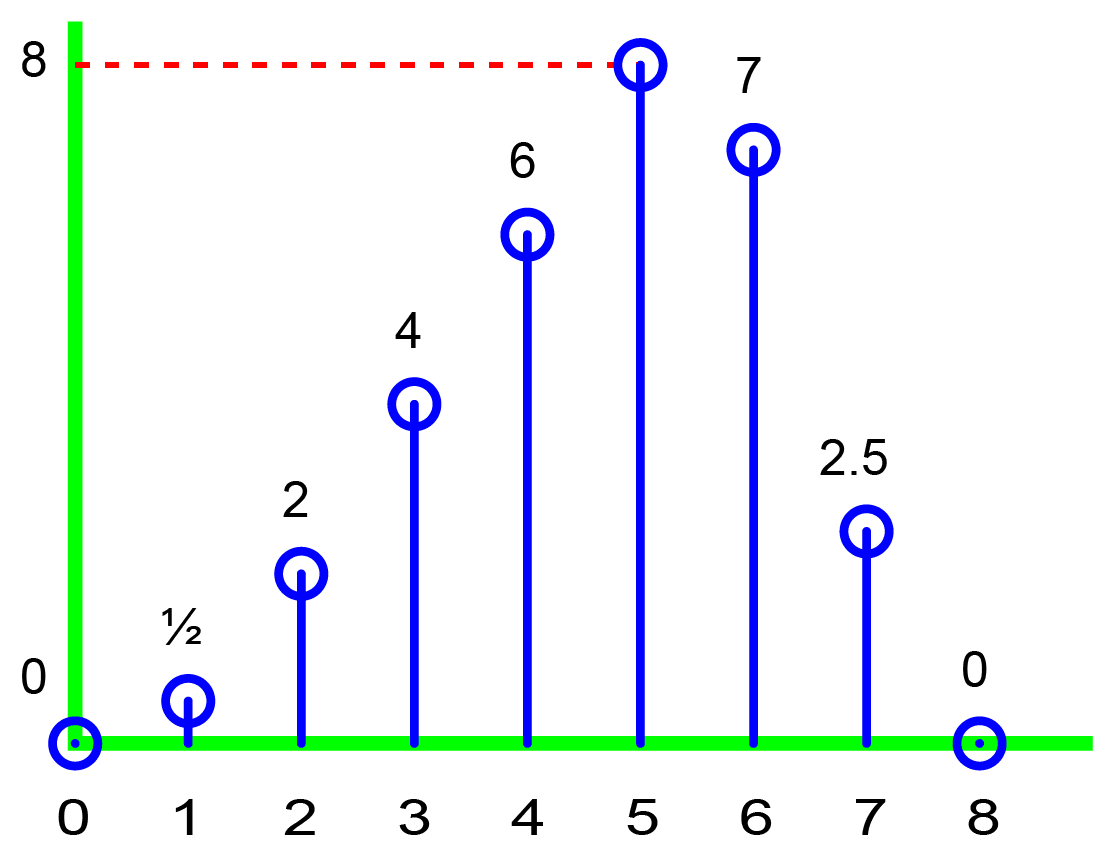
Window convolved with data (“filtering”)
Heisenberg Uncertainty Principle
Multiplying a window function with a data sequence in time results in a distortion in frequency. The FFT of the windowed waveform will be similar to that of the original but will have been altered. In general, the larger the window in time, the less distortion in frequency.
The Heisenberg uncertainty principle sums up this conflict. Increased resolution in time results in decreased resolution in frequency (more distortion); decreased resolution in time results in increased resolution in frequency (less distortion).
Characteristics of Window Functions
For each window size, a window function results in different spectral leakage and resolution characteristics. All window functions are well defined in both time and frequency domains. The characteristics of the resulting spectral behavior depend on the definition of the selected window function.
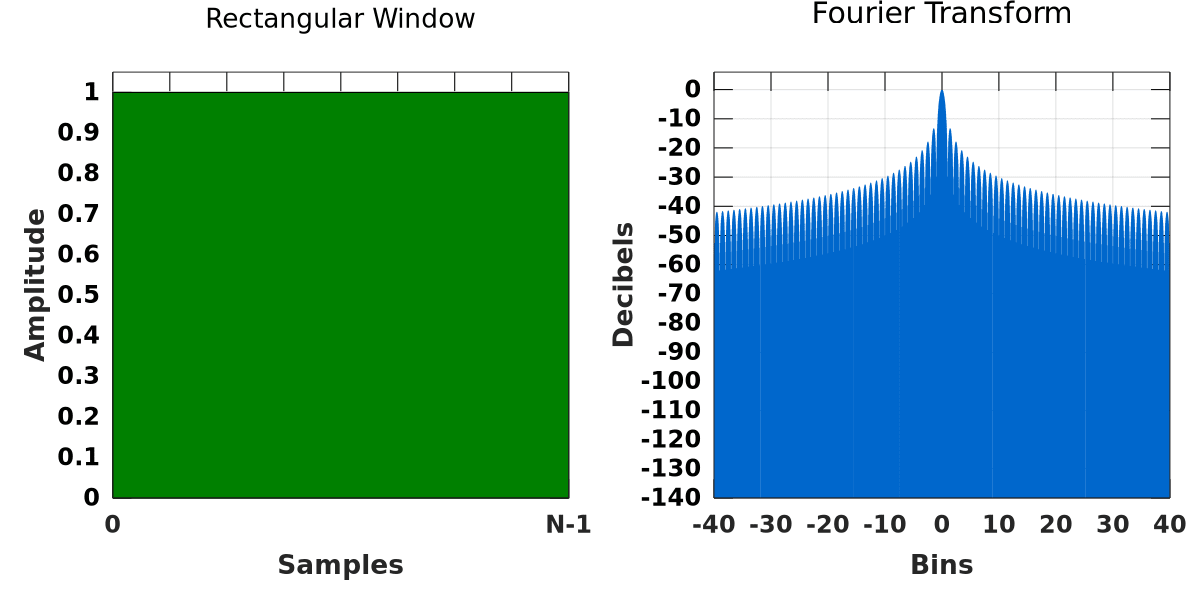
Cropping the data is not an escape from the windowing dilemma—cropping is mathematically equivalent to multiplying by a rectangular window. Rectangular windows have poor spectral properties, producing high leakage, which motivates the use of alternative window functions.
Window Function Selection Process
If you are searching for the exact amplitude of the signal, then the optimal choice is the flat top window, as it exhibits the best amplitude resolution. If you are searching for the exact frequency of the peaks of a signal—and it has the length needed to avoid discontinuities—then the rectangular window is ideal.
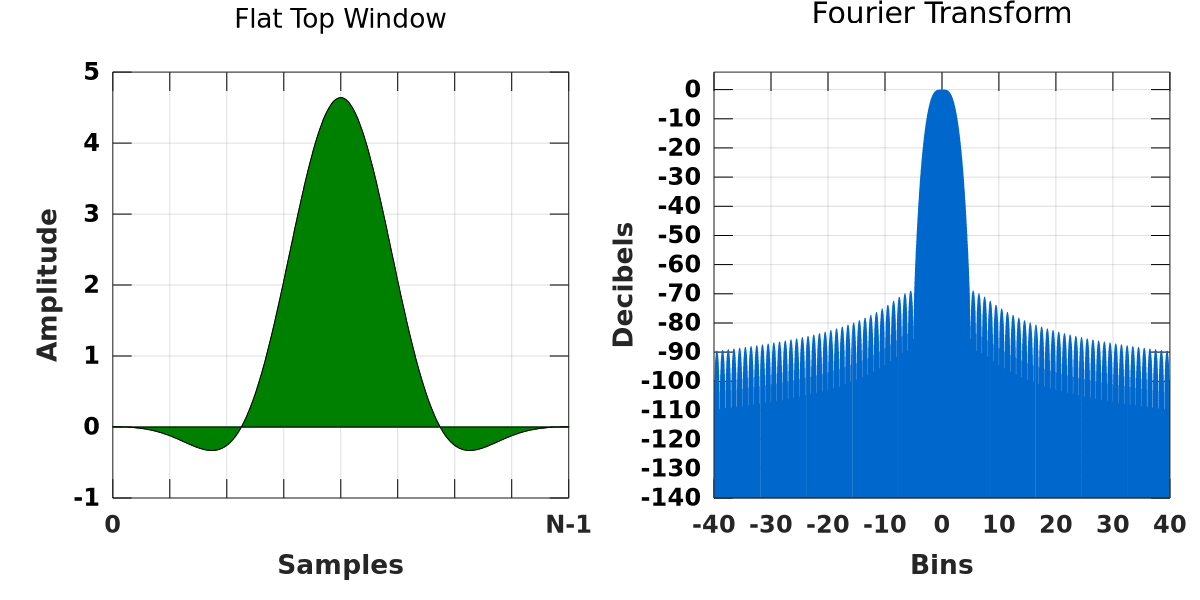
Otherwise, the Blackman, Hamming, or Hanning windows perform well. Each has certain advantages and disadvantages when compared to the other two.
For example, the Hamming has a superior side lobe height to the Hanning but a worse side lobe roll-off rate. The Blackman is a combination of the other two windows with a better side lobe roll-off rate to the Hanning and a superior side lobe height to both windows. Consequently, the Blackman has a wider main lobe width.
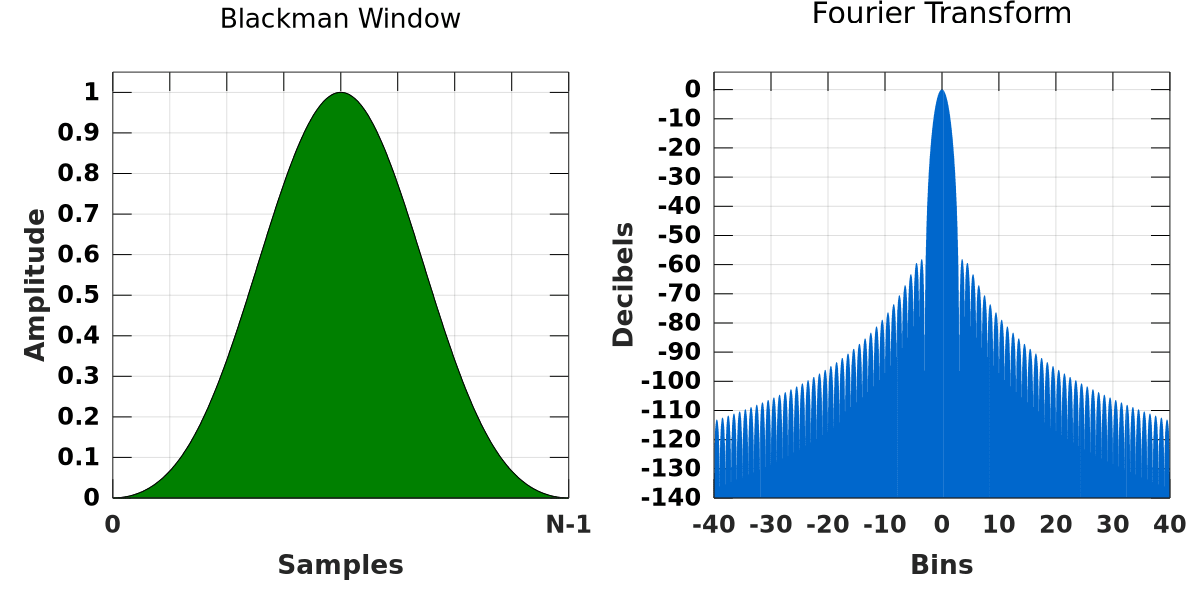
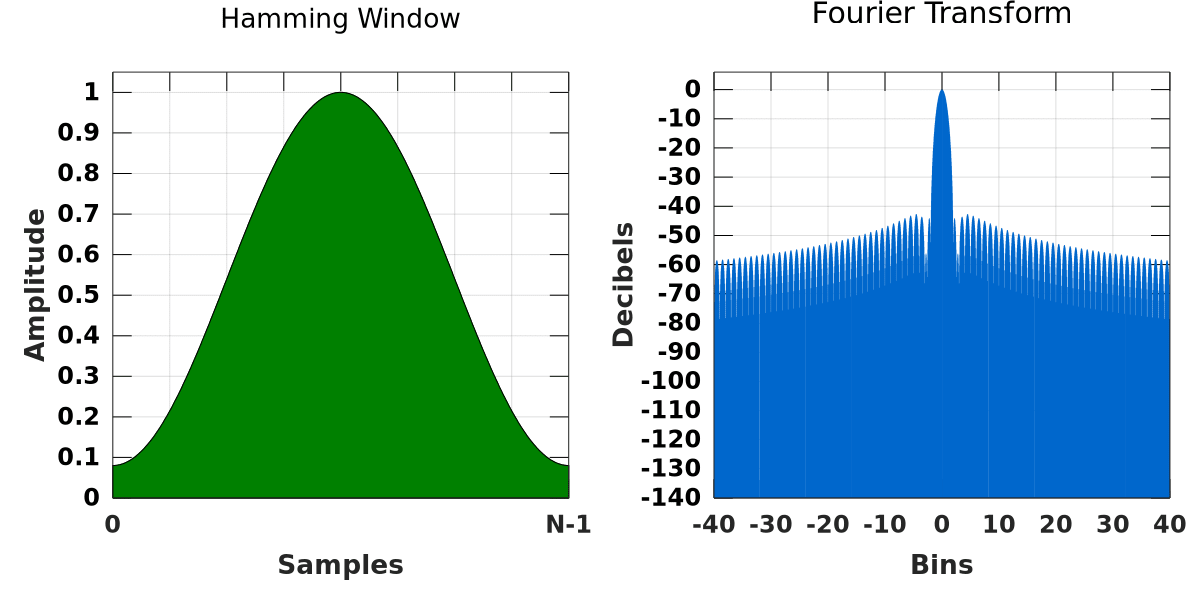
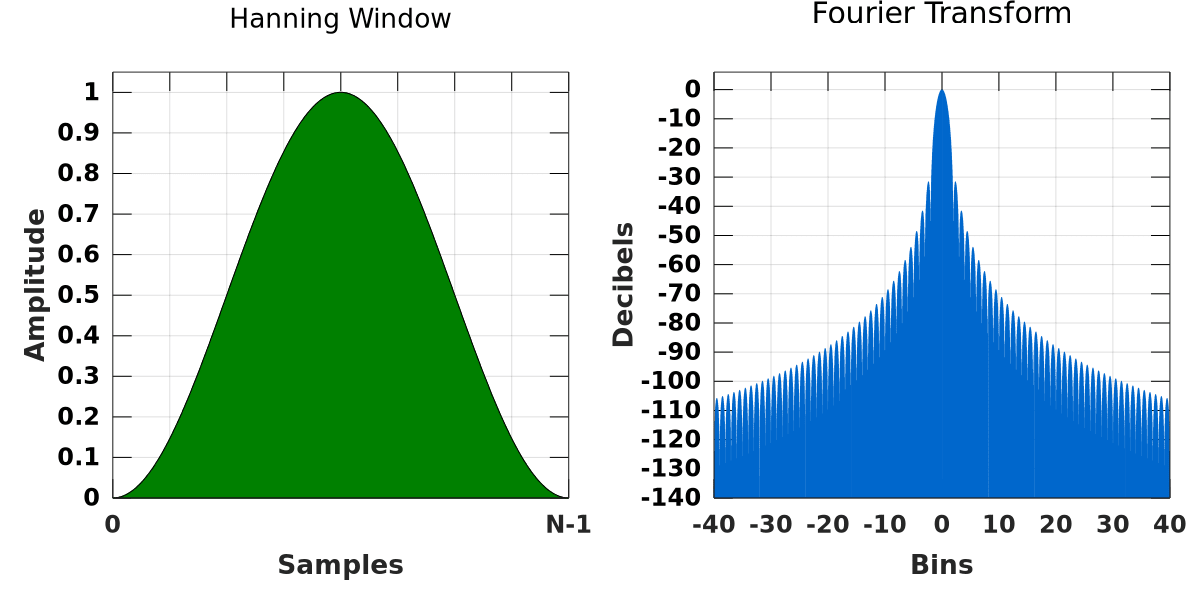
All windows compromise these metrics, and it is up to the user to decide which metrics are important and which can be sacrificed.
Examples
Two signals are close in the frequency domain: one is at 50Hz and the other at 51Hz.
The user wants to choose a window function with a narrow main lobe width because they have better selectivity for finding closely spaced signals. In this case, a lower side lobe height is more important than a superior side lobe roll-off rate.
Between the Blackman, the Hanning, and the Hamming, the user rules out the Blackman because it has a wider main lobe width. They also prefer the Hamming over the Hanning, as it has a lower side lobe height.
If the two signals are far apart (500Hz and 1,000Hz), then the main lobe width is less important, and the side lobe roll-off rate is more important than the side lobe height. In this case, the side lobe roll-off rate has the space for a greater effect.
Yet, this doesn’t mean that the main lobe width or side lobe height is unimportant, and it is wise to optimize both. When attenuation (side lobe roll-off rate and side lobe height) is more important than selectivity (main lobe width), the user chooses the Blackman because it prioritizes selectivity over attenuation.
Other Considerations
- The rectangular window is the optimal choice if the user can choose a window length with no signal discontinuities. This window does not distort the spectral representation of the signal when there are no discontinuities.
- The industry standard minimum side lobe height is approximately -45dB.
- The equivalent noise bandwidth (ENBW) represents the width of a rectangle in bins. Its area is equivalent to the energy of the respective window. A lower ENBW is ideal because less noise is inserted into the spectral representation of the signal.
Filtering, windowing, and the FFT are necessary to analyze frequency content accurately. The FFT converts a time-domain signal into the frequency domain, whereas filtering and windowing effects influence spectral resolution and accuracy. Proper selection of filters and windows optimizes FFT results, minimizing distortions in vibration analysis.
