Kurtosis

March 29, 2018

Kurtosis describes the deviation of a data set’s peak values from the mean. It calculates the signal’s average deviation from the mean to the fourth power divided by the standard deviation to the fourth power. Equation 8 gives the kurtosis for a set of numbers, x_n, n = 1, …, N.

(1) $\begin{equation*} \kappa=\frac{1}{N\sigma^2}\sum_{n=1}^{N}(x_{n}-\mu)^4 \cong \frac{\frac{1}{N} \sum_{n=1}^{N} (x_{n}-\bar{x})^4}{(\frac{1}{N} \sum_{n=1}^{N} (x_{n}-\bar{x})^2)^2} \end{equation*}$

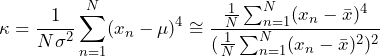
Equation 8

Kurtosis is dimensionless, meaning it has not units. For a random variable with normal (Gaussian) distribution, k = 3. For example, the turbulent pressure signal in Figure 3.3 has a value of k = 2.6, which is near the expected value.

Some computer programs calculate the excess kurtosis value as k – 3. In this case, a normal distribution would have an excess of 0.

Probability Distribution

Kurtosis is a ratio of statistical moments, which are parameters that describe the shape of a data distribution. More specifically, it is the fourth statistical moment divided by the square of the second statistical moment (variance). A data set’s statistical moments define its probability distribution.

On a graph of a data set’s distribution, the kurtosis measures the distribution “tails.” A data set with a high k value will have a distribution curve with a higher peak value at the mean and longer tails. In other words, more data points will be at the extreme values from the mean.

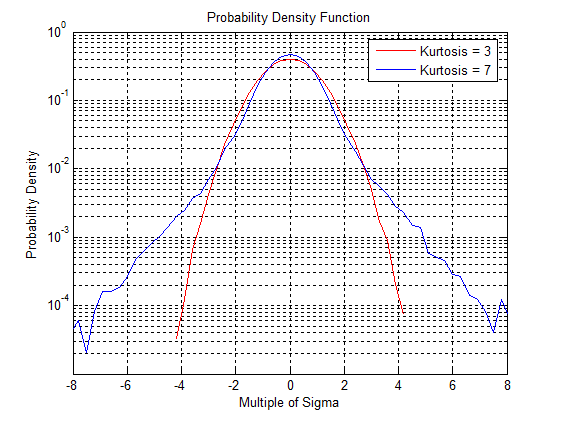
A comparison of two probability density functions with different kurtosis values. The red line with narrower tails represents a kurtosis of 3. The blue line with wider tails represents a kurtosis of 7.

Comparison of two data sets’ distributions with different kurtosis values.

High k: A sharper peak and heavier tails; more values near the mean and extremes
Low k: A flatter peak and lighter tails; fewer extreme values and a more uniform distribution

Kurtosis helps identify outliers and assess the damage potential of vibration data. In many engineering applications, a higher value suggests more damaging events, as the data spend more time near extreme values.