Transmissibility

Back to: Fundamentals of Signal Processing

A transfer function, H, can uncover a resonance or anti-resonance in a system. Transmissibility T_yx(f) of a signal pair x and y is as follows, where S_yy is the PSD of y and S_xx is the PSD of x.

(1)  

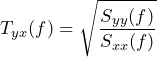
One should consider using transmissibility if they are not concerned with the statistical relationship between x and y or if there is not a statistical relationship at all. It is also helpful for determining a value between Ĥ₁ and Ĥ₂, such as Ĥ_v.

When not to Use Transmissibility

Transmissibility is not the best option if the goal is complex-valued system response data. Unlike all other transfer functions, transmissibility is real-valued and not complex-valued.

• T_yx(f) ≜ Ŝ_yy(f) / Ŝ_xx(f) (real ÷ real = real)
• Ĥ₁(f) ≜ Ŝ_yy(f) / Ŝ_yx(f) (real ÷ complex = complex)

One should also not use transmissibility if they are concerned with the statistical relationship between x and y. Unlike all other transfer functions, transmissibility does not directly consider cross-statistical properties between x and y, it only uses the auto-statistical properties of x with x and y with y.

In particular, T_yx does not use the cross-spectral density of x and y; rather, it only uses the auto-spectral density (PSD) of x and PSD of y.

Insights

1. For a linear time invariant (LTI) system with frequency response H(f):

(2)  

In the case of an LTI system, the transmissibility of x and y is equivalent to the magnitude of the frequency response |H(f)|.

2. T_yx is the geometric mean of Ĥ₁ and Ĥ₂ because T_yx is, in some sense, between Ĥ₁ and Ĥ₂.

(3)  

If there is noise on both input and output, then T_yx is an alternative to Ĥ_v, which is also between Ĥ₁ and Ĥ₂.