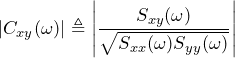Coherence

June 2, 2021

Back to: Fundamentals of Signal Processing

There are two definitions of coherence in literature: complex and ordinary.

Complex:

(1) $\begin{equation*} C_{xy}(\omega)=\frac{S_{yx}(\omega)}{\sqrt{S_{xx}(\omega)S_{yy}(\omega)}} \end{equation*}$

Ordinary:

(2) $\begin{equation*} \gamma_{xy}^2(\omega)=\frac{|S_{yx}(\omega)|^2}{S_{xx}(\omega)S_{yy}(\omega)} \end{equation*}$

Where:

- S_xx(f) is the PSD of x
- S_yy(f) is the PSD of y
- S_yx(f) is the CSD of x and y

ObserVIEW currently offers complex coherence. To calculate ordinary coherence, take the magnitude squared of the complex coherence.

Notes

Of the two definitions, ordinary coherence is more common in literature. However, ordinary coherence is the magnitude squared of complex coherence.

(3) $\begin{equation*} \gamma_{yx}^2=|C_{yx}(f)|^2 \end{equation*}$

Thus, ordinary coherence is a special case of the more general complex coherence.

Applications

Ordinary coherence has two main practical uses.

Coherence is a measure of confidence that a peak observed in a transfer function is a resonant frequency of the device under test and not a spike due to measurement noise. For example, suppose that a peak at frequency f in a transfer function is observed. Then:

γ_yx²		\|C_yx\|	Description
γ_yx²≥ 0.70	or	\|C_yx\|≥ 0.85	High degree of confidence
γ_yx²≤ 0.50	or	\|C_yx\| ≤ 0.707	Not likely
0.50 < γ_yx²< 0.70	or	0.707 < \|C_yx\| < 0.85	Somewhat likely

Coherence is a measure of linearity of the system under test at frequency f.

An ordinary coherence value near 1 indicates that the system is linear-time-invariant (LTI) at frequency f. An ordinary coherence value near 0 indicates that the system is non-linear, statistically changing with time or both.

Coherence drops within a resonance, and one must evaluate surrounding coherence values to make a sound judgment.

Coherence as a Measure of Linearity

In many cases, the signal x may represent an input to a system and the signal y may represent the output. Suppose that an input to a system results in a response h[n] and that the DTFT of the response is H(ω). If the system is LTI, then S_yx(ω) = H(ω) S_xx(ω) and S_yy(ω) = |H(ω)|² S_xx(ω).

Also, the coherence will be:

(4) $\begin{equation*} |C_{xy}(\omega)|\triangleq\left|\frac{S_{xy}(\omega)}{\sqrt{S_{xx}(\omega)S_{yy}(\omega)}}\right| \end{equation*}$

by definition of coherence C_xy

(5) $\begin{equation*} =\left|\frac{H(\omega)S_{xx}(\omega)}{\sqrt{S_{xx}(\omega)S_{yy}(\omega)}}\right| \end{equation*}$

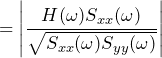
(6) $\begin{equation*} =\frac{|H(\omega)|S_{xx}(\omega)}{\sqrt{S_{xx}(\omega)S_{yy}(\omega)}} \end{equation*}$

(7) $\begin{equation*} =\frac{|H(\omega)|S_{xx}(\omega)}{\sqrt{S_{xx}(\omega)|H(\omega)|^2S_{xx}(\omega)}} \end{equation*}$

(8) $\begin{equation*} =1 \end{equation*}$

Thus, for an LTI system, the ordinary coherence γ_yx²(f) will be 1 for all frequencies. In contrast, if the coherence is less than 1, then it is not LTI. Further, if γ_yx²(f) is 1 at certain frequencies, then the system is LTI at those frequencies.

Coherence as a Measure of Confidence in Transfer Function H₁

If a system is LTI with a frequency response of S_yx(ω) = H(ω) S_xx(ω), then H(ω) = S_yx(ω)/S_xx(ω), which is the transfer function H₁. Thus, if one wants a measure of how good an estimator H₁ is likely to be, they can check the ordinary coherence function γ_yx²(f).

If γ_yx²(f) is 1 for all or nearly all frequencies, then H_yx1(f) is likely a good H_yx1 estimator. If γ_yx² is close to 0, then one should be much less confident about the quality of the H_yx1 estimator.

Coherence as a Measure of Distance Between H₁ and H₂

You can also view the ordinary-coherence function γ_yx²(f) as a measure of the distance between H_yx1 and H_yx2.

(9) $\begin{equation*} \gamma_{yx}^2=\frac{|S_{yx}|^2}{[S_{xx}S_{yy}]}=\frac{[S_{yx}S_{yx}]}{[S_{xx}S_{yy}]}=\frac{[S_{yx}(f)/S_{xx}]}{[S_{yy}/S_{yx}]}=\frac{H_{1}}{H_{2}} \end{equation*}$

As 0 ≤ γ_yx²(f) ≤ 1, then 0 ≤ |H₁/H₂| ≤ 1. Therefore, |H₁(f)| ≤ |H₂(f)|.

When the true H is LTI, then H₁=H₂—meaning the distance is 0— and γ_yx²=1. If H is not LTI, then the distance will be greater than 0 and γ_yx²<1.

In the above example, the distance between |H₁(435)|=19 and |H₂(435)|=607 is great. This is reflected in the following equation:

γ_yx²(435) = |C_yx(435)|² = (0.007)² =(0.0098)² = (19/607)² = (|H₁|/|H₂|)²

Note of Caution

As the name implies, estimators yield estimates. In general, these estimates contain some error compared to the true value. It would be difficult to find a more striking example of this situation than the K=1 Welch estimate of coherence.

Welch Estimate of Coherence

Compare the rectangular window K=1 Welch estimate of coherence with the true coherence of uncorrelated white noise signals. If:

x[n] and y[n] are zero-mean white noise sequences
x[n] and y[n] are uncorrelated with each other
The estimate Ĉyx (ω) is the K=1 Welch estimate of x and y

Then, Ĉyx(ω)= 1.

Proof:

(10) $\begin{equation} \gamma_{yx}^2=\frac{\|S_{yx}\|^2}{S_{xx}S_{yy}} \end{equation}$	by definition of ordinary coherence γ_yx(ω)
(11) $\begin{equation} =\frac{\|[F_{x}(n)][F_{y}(n)]^\|^2}{\|F_{x}(n)\|^2\|F_{y}(n)\|^2} \end{equation*}$	by Welch algorithm

(12) $\begin{equation*} =\frac{|[F_{x}(n)]|^2|[F_{y}(n)]|^2}{|F_{x}(n)|^2|F_{y}(n)|^2} \end{equation*}$

(13) $\begin{equation*} = 1 \end{equation*}$

Thus, the K=1 Welch estimate of coherence is always 1. It is an estimate, but is it a good estimate? To answer this question, we can compute the true (non-estimated) coherence.

(14) $\begin{equation} \gamma_{yx}^2=\frac{\|S_{yx}\|^2}{S_{xx}S_{yy}} \end{equation}$	by definition of ordinary coherence γ_yx(ω)
(15) $\begin{equation} =\frac{\|FR_{yx}(m)\|^2}{S_{xx}S_{yy}} \end{equation}$	by definition of CSD S_yx(ω)
(16) $\begin{equation} =\frac{\|FE\lceil x(m)y^(0)\rceil\|^2}{S_{xx}S_{yy}} \end{equation*}$	by definition of cross-correlation R_yx(m)
(17) $\begin{equation} =\frac{\|F\{E\lceilx(m)\rceil E\lceily^(0)\rceil\}\|^2}{S_{xx}S_{yy}} \end{equation*}$	x and y are uncorrelated
(18) $\begin{equation} =\frac{\|F\{0\times0\}\|^2}{S_{xx}S_{yy}} \end{equation}$	x[n] and y[n] are zero-mean
(19) $\begin{equation} \gamma_{yx}^2=0 \end{equation}$	because the Fourier transform F of 0 is 0

The true value of the coherence is γ_yx(ω)= 0, but the Welch estimate is γ_yx(ω)= 1. In many cases, Welch will likely yield a good estimate. However, as the above example demonstrates, this is not always the case, and some caution is necessary.