Scaled Transfer Function Estimator

Back to: Fundamentals of Signal Processing

The scaled transfer function estimator Ĥ_s(f) with scaling factor s (where 0 ≤ s ≤ ∞) is an estimate of the true transfer function H(f) of a system.

The scaling factor is the ratio of output noise power to input noise power such that s² = Ŝ_yy/Ŝ_xx. This is with the assumption that Ŝ_xx(f) and Ŝ_yy(f) are constant with respect to frequency f.

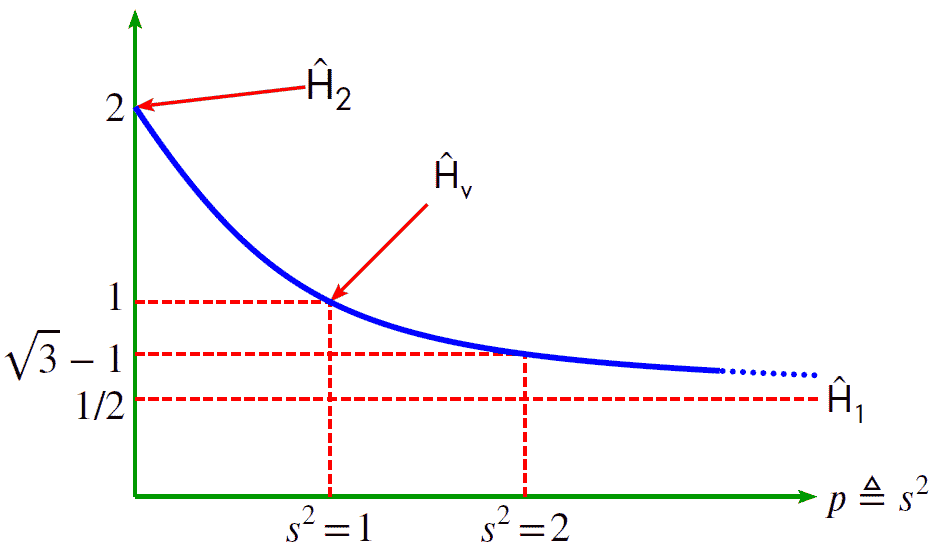
Ĥ_s is a generalization of the transfer function estimators Ĥ₁, Ĥ₂, and Ĥ_v. Ĥ_s is defined as:

(1)  

Alternate Forms

Using the technique of rationalizing the denominator—or, in this case, rationalizing the numerator—we can arrive at alternate and useful forms for Ĥ_s. Particularly, if we multiply numerator and denominator by the rationalizing factor, we can arrive at the following equation:

(2)  

Moreover, if we divide the numerator and denominator by s², we get:

(3)  

Special Cases of Ĥ_s

Ĥ₁, Ĥ₂, and Ĥ_v are special cases of Ĥ_s. Using the definition of Ĥ_s, we see Ĥ_s=0=Ĥ₂ and Ĥ_s=1=Ĥ_v. Using the second alternate form, we see Ĥ_s➜∞=Ĥ₁.