Complex Numbers

Back to: Fundamentals of Signal Processing

A complex number z is an ordered pair of two real numbers a and b. There are three standard ways to represent z. Put another way, there are three numerals that represent the identical number z:

1. Ordered pair (a, b)

Example: z = (√3, 1)

2. Rectangular coordinates a + in

Example: z = √3 + i1

3. Polar coordinates |z|∠z

Example: z = |z|∠z = 2e^iπ/6

In the three representations:

• a is the real part of z
• b is the imaginary part of z
• |z| is the magnitude of z
• ϕ=∠z is the phase of z

While the compound quantities (a,b) and ze^iϕ are complex numbers, all the components (a, b, |z|, and ϕ) are real numbers.

Graphical Representation of Complex Numbers

A complex number is an ordered pair z=(a, b), so it is convenient to represent it on a two-dimensional graph where the real part a is the abscissa (x-axis) and the imaginary part b is the ordinate (y-axis).

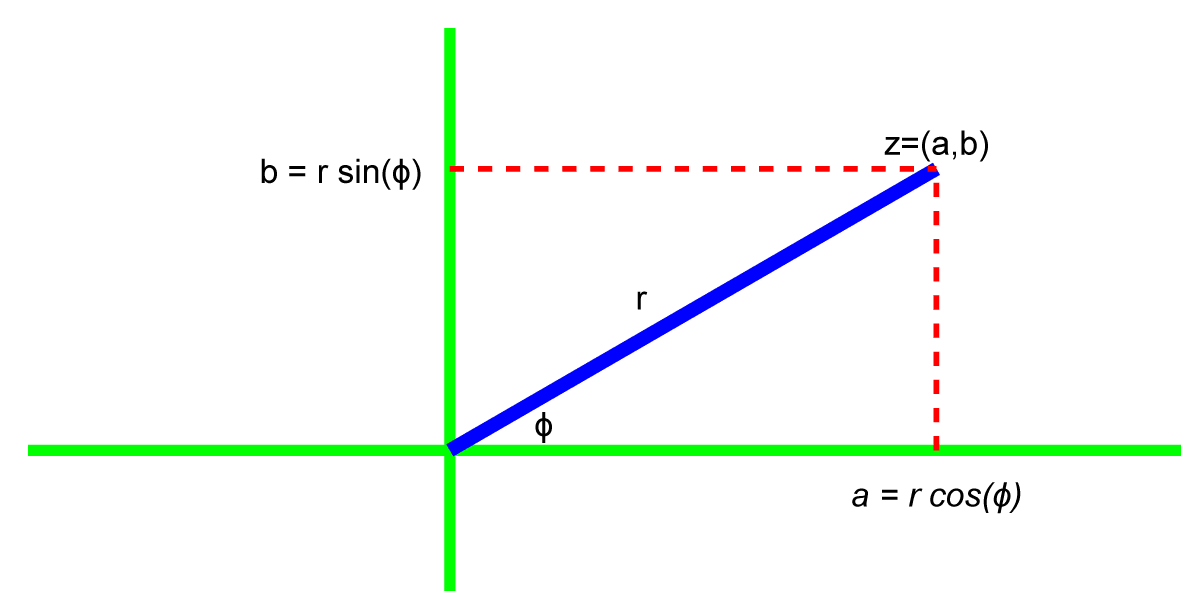
Conversion Between Representations

Trigonometric definitions and two common theorems make for easy conversion between the three representations of z:

• Tangent function: tan(ϕ) = b/a
• Arctangent function: ϕ = atan(b/a)
• Pythagoras’ theorem: r² = a² + b²
• Euler’s identity: e^iϕ = cos(ϕ) + isin(ϕ)

Examples

If: z = (a,b) = (√3, 1) = √3 + i
Then: r = sqrt[(√3)² + (1)²] = √[10] ≈ 3.16
And: ϕ = atan(√3/1) = π/6 (30°)

If: z = (a,b) = (4, 3) = 4 + 3i
Then: r = sqrt[4² + 3²] = sqrt[25] = 5
And: ϕ = atan(3/4) ≈ 0.644 (36.9°)

If: z = (a,b) = (-4, 3) = -4 + 3i
Then: r = sqrt[4² + 3²] = sqrt[25] = 5
And: ϕ = atan(-3/4) ≈ π-0.644 (180°-36.9°=143.1°)

Star-algebra Structure

Complex numbers with the conjugate operator * is a special case of a star-algebra. The conjugate z* of a complex number z=a+ib is defined as z* = a – ib, where z = a + ib.

Using the conjugate operator, it is easy to extract the real and imaginary components from a complex number z = a + ib:

• Real part of z= [1/2](x + x*) because x+x* = (a+ib)+(a-ib)=2a
• Imaginary part of z= [1/2](x – x*)because x-x* = (a+ib)-(a-ib)=2b