What is Frequency?

Back to: Fundamentals of Signal Processing

Waveforms that change rapidly are said to be high frequency. For example, if a bus stops at a station 10 times per hour, we might say that it arrives frequently. By this, we mean that the bus’s schedule is characterized by many cycles per hour. In essence, this captures the idea of high frequency: many cycles per unit time.

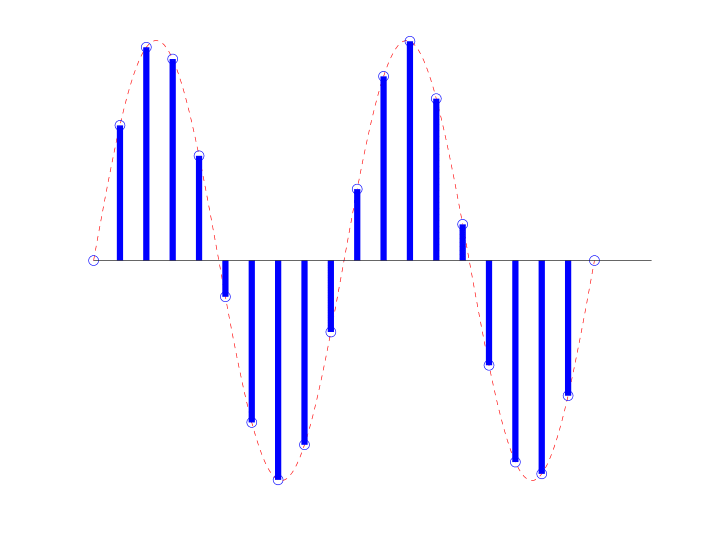
Waveforms that change slowly are said to be low frequency. To follow the same example, if the bus stops at a station one time per 10 hours, we might say that it arrives infrequently—the bus’s schedule is characterized by very few cycles per hour.

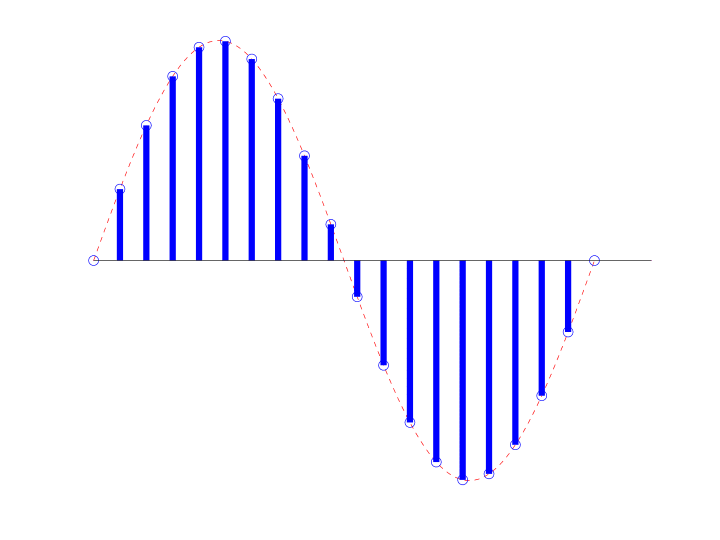
A waveform that does not change at all is often referred to as direct current (DC). If the bus breaks down and is always at the station, we might say that its presence is a kind of constant—it does not go through any cycles. This scenario encapsulates the idea of DC: zero cycles per unit time or a constant.

Considerations

The focus of frequency is cycles per time. Beyond this, we want a concise function that represents a given frequency. The function should be cyclic, but there are many cyclic functions. Which one do we choose?

Arguably, the ideal function to represent frequency is the sinusoid: sines and cosines.

Slope

The idea of cycles per time of a function is related to the idea of the slope. A function cannot go through many cycles per second when it is changing very slowly–i.e. when its slope is small.

The geometric concept of slope is related to the analytic concept of differentiation or “taking the derivative.” Differentiation (d/dt) is fundamental to the natural order of the universe.

Suppose you have a function f(t) where f”(t) + f(t) = 0. f” is the second derivative of f and f’ is the first derivative. Then:

• If f(0)=1 and f'(0)=0, then f(t) must equal cos(t).
• If f(0)=0 and f'(0)=1, then f(t) must equal sin(t).

Differential Operator

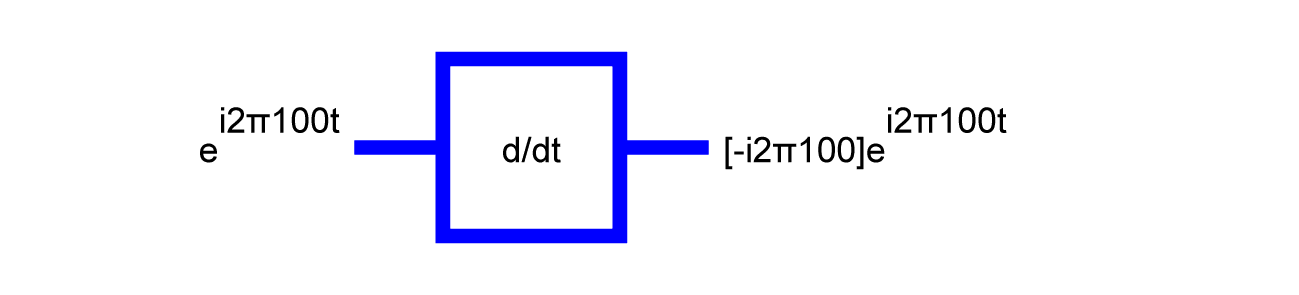
Sinusoids are eigenvectors for the differentiation operator.

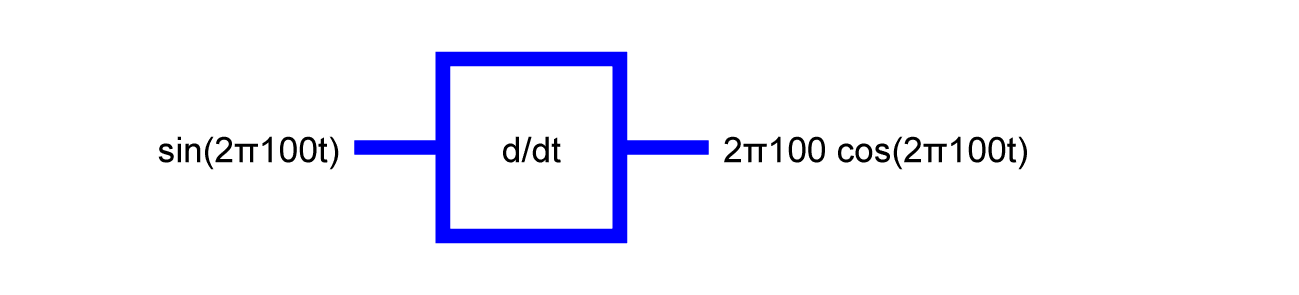
A 100Hz sine in yields a phase that is shifted 100Hz sine out. The eigenvalue is 2π100.

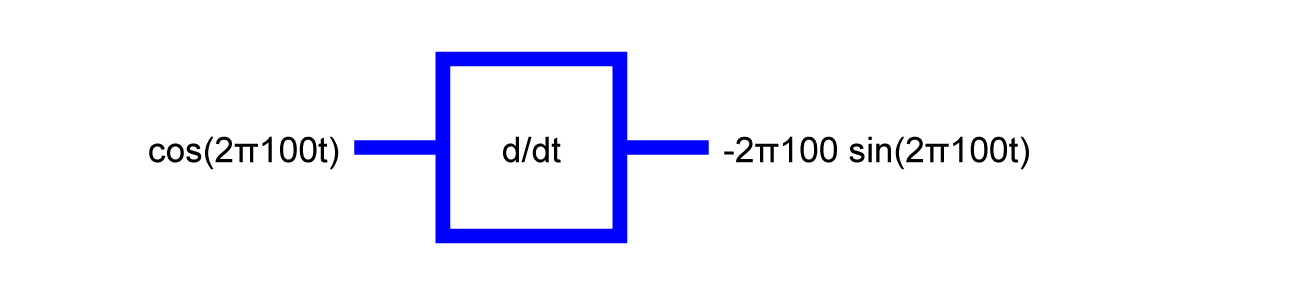
A 100Hz cosine in yields a phase that is shifted 100Hz cosine out. The eigenvalue is -2π100.

A 100Hz sine in yields a 100Hz sine out. The eigenvalue is -(2π100)2.

A 100 Hz complex exponential in yields a 100 Hertz complex exponential out. The eigenvalue is -i2π100.

Linear Time-Invariant System

Sinusoids are also eigenvectors for any linear time-invariant (LTI) system.

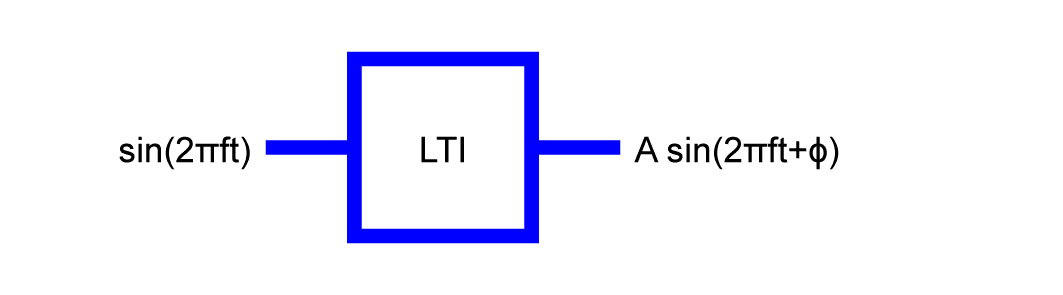
A sinusoid in yields a sinusoid out at the same frequency. The phase and amplitude may change, but no other frequency component will be generated.