Coherence MATLAB Resources
March 27, 2019
Transfer Function
Coherence
Cross Spectral Density
Back to: Mathematics for Understanding Waveform Relationships
MATLAB® offers operators supporting several statistical estimators using Welch’s method. These include the following:
|
|
mscohere(…) |
Estimate ordinary coherence. |
|
|
|
pwelch(…) |
Estimate power spectral density. |
|
|
|
cpsd(…) |
Estimate cross power spectral density. |
Example Code from MATLAB
Complex coherence can be calculated in MATLAB using cross-spectral density (CSD) and power spectral density (PSD) as demonstrated below.
clear % clear all variables
format long g; % set format of text output
N = 16; % length of input data sequence x
Fs = 1; % sample rate (used for scaling)
percent = 50; % percent overlap
Nfft = N * (1-percent/100);
x= [0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0]';
y= [0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0]';
% 0 3 7 11 13 15
%----------------------------------------------------------------------------
% smoothing window
%----------------------------------------------------------------------------
window = hanning(Nfft); % Hanning window
%----------------------------------------------------------------------------
% calculate estimates
%----------------------------------------------------------------------------
[Sxy,freq]=cpsd( x,y,window,Noverlap,Nfft,Fs); % estimate Sxy
[Sxx,freq]=pwelch( x, window,Noverlap,Nfft,Fs); % estimate Sxx
[Syy,freq]=pwelch( y,window,Noverlap,Nfft,Fs); % estimate Syy
[Cms,freq]=mscohere(x,y,window,Noverlap,Nfft,Fs); % estimate ordinary coherence
% | | | | | | | | |_____ sample rate
% | | | | | | | |_________ estimate length
% | | | | | | |_________________ num. overlapping positions
% | | | | | |__________________________ window type
% | | | | |_____________________________ data sequence y
% | | | |_______________________________ data sequence x
% | | |_____________________________________ estimation operation
% | |__________________________________________ x-axis sequence
% |_________________________________________________ estimate sequence
Cxy = Sxy ./ sqrt( Sxx .* Syy ); % estimate complex coherence
%----------------------------------------------------------------------------
% perform integrity check
%----------------------------------------------------------------------------
if norm(Cms-abs(Cxy).^2)<1e-12
fprintf("Cxy integrity check OK!n");
else
fprintf("Cxy integrity check FAILED!!!n");
end
A Note of Caution
As the name implies, estimators yield estimates. In general, these estimates contain some error with respect to the true value.
It would be difficult to find a more striking example of this situation than the K=1 Welch estimate of coherence. To understand this, compare the rectangular window K=1 Welch estimate of coherence with the true coherence of uncorrelated white noise signals:
If:
- x[n] and y[n] are zero-mean, white noise sequences
- x[n] and y[n] are uncorrelated
- the estimate Ĉxy (w) is the K=1 Welch estimate of x and y
Then:
(1) ![]()
Proof:
(2) 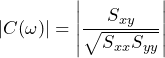
(3) 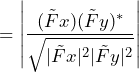
(4) ![]()
Thus, the K=1 Welch estimate of coherence is always 1! This is definitely an estimate; but the question is, “Is it a good estimate?”
To answer this question, let’s compute the true (non-estimated) coherence:
|
(5) |
by definition of coherence Cxy(ω) |
|
(6) |
by definition of cross-correlation Rxy |
|
(7) |
because x[n] and y[n] are uncorrelated |
|
(8) |
because x[n] and y[n] have mean=0 |
|
(9) |
because the Fourier transform of 0 is 0 |
So, we see that the true value of the coherence is Cxy(ω)= 0 (the smallest possible value), but the Welch estimate is Ĉxy(ω)= 1 (the largest possible value). It is likely that, in most cases, Welch will yield a very “good” estimate. However, as the above example demonstrates, this is not always the case and some caution is in order.
