CoursesCertificatesBack to VR.com

MENU

Z-transform

June 2, 2021

Back to: Fundamentals of Signal Processing

The z-transform is defined as:

(1)   \begin{equation*} X(\omega)=\sum\nolimits_{n\in\mathbb{Z}}x(n)z^{-n} \end{equation*}

Unit Circle in Z-domain

The z-transform is a generalization of the discrete-time Fourier transform.

(2)   \begin{equation*} X(\omega)=\sum\nolimits_{n\in\mathbb{Z}}x(n)e^{-i\omega n} \end{equation*}

Therefore, the DTFT is the unit circle portion of the z-transform.

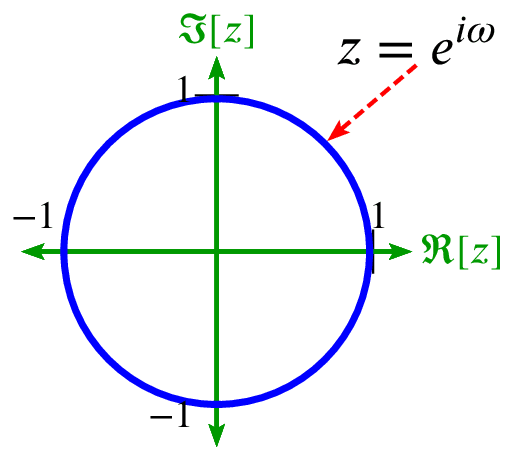
z-domain unit circle

The N-point DFT or FFT is N samples around the unit circle. The Fourier transform, which is a special case of the s-domain Laplace transform, can be roughly mapped into the z-plane by use of the bilinear transform.

(3)   \begin{equation*} s=2F_{s} \end{equation*}

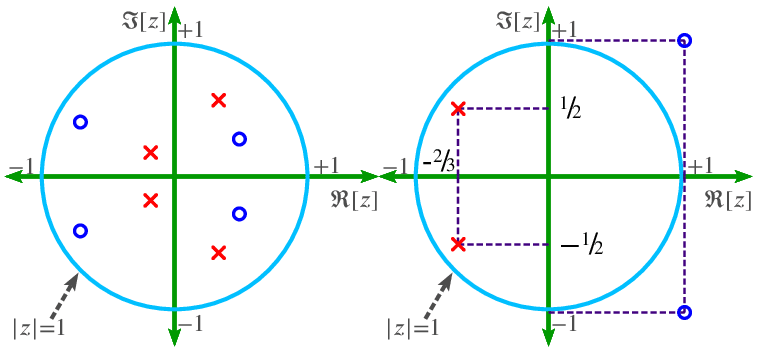
Pole-zero Locations

The roots of the numerator are called zeros, and the roots of the denominator are called poles.

(4)   \begin{equation*} H(z)=\frac{3/2z^2+5/2z+7/2}{z^2+5z+6}\times\frac{z^{-2}}{z^{-2}} \end{equation*}

(5)   \begin{equation*} =\frac{3/2+5/2z^{-1}+7/2z^{-2}}{1+5z^{-1}+6z^{-2}} \end{equation*}

z-domain poles and zeros

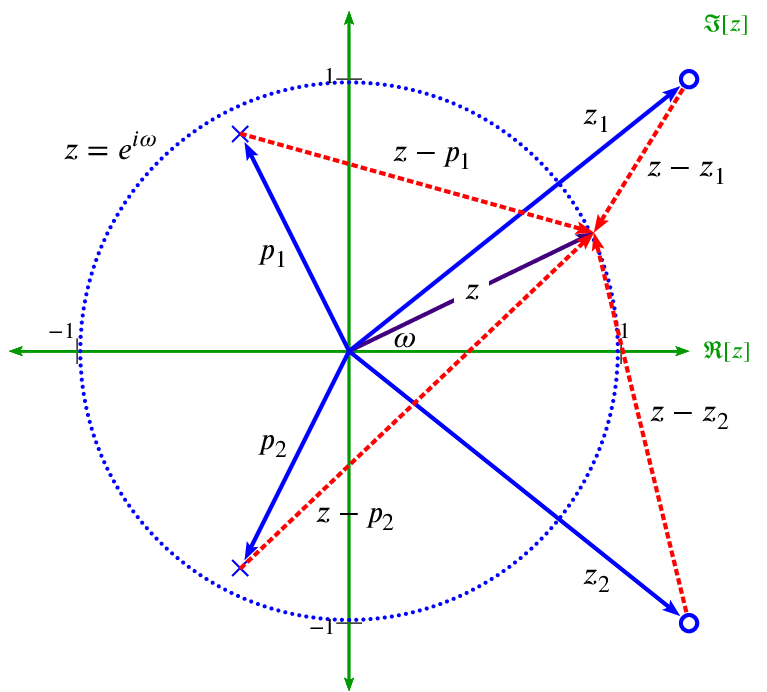
Determine Frequency Response

The frequency response of a filter is determined by the interaction of a unit vector rotating around the unit circle with the poles and zeros of the filter.

  • The unit vector at rotation ω=0 corresponds to DC (0Hz).
  • The unit vector at rotation ω=π (180°) corresponds to Fs/2 or the Nyquist frequency.

When the tip of the unit vector gets close to a zero, the filter magnitude response is pushed downwards because zero is a root of the numerator polynomial. When the tip of the unit vector gets close to a pole, the filter magnitude response is pushed upwards because a pole is a root of the denominator polynomial.

z-domain frequency response

Pole-zero locations are important for:

  • Wavelets
  • Symlets
  • B-splineis

z-domain wavelets