CoursesCertificatesBack to VR.com

MENU

Scaled Transfer Function Estimator

May 24, 2019

Back to: Mathematics for Understanding Waveform Relationships

The scaled transfer function estimator Ĥs(f) is an estimate of a system’s true transfer function with scaling factor s, where 0 ≤ s ≤ ∞.

The scaling factor s is the ratio of output noise power to input noise power such that Ŝ = Ŝyy / Ŝxx. This assumes that Ŝxx(f) and Ŝyy(f) are constant with respect to frequency f (x and y are white noise sequences.)

Ĥs is a generalization of the transfer function estimators Ĥ1, Ĥ2, and Ĥv.

Ĥs is defined as:

(1)   \begin{equation*} \frac{\~{S}_{yy}(\omega)-s^2\~{S}_{xx}(\omega) + \sqrt{[\~{S}_{yy}(\omega)-s^2\~{S}_{xx}(\omega)]^2 + 4s^2|\~{S}_{xy}(\omega)|^2}}{2\~{S}_{xy}(\omega)} \end{equation*}

Alternate Forms

Using the technique of “rationalizing the denominator” (or, in this case, “rationalizing the numerator”), we can arrive at alternate and useful forms for the scaled transfer function estimator. Particularly, if we multiply the numerator and denominator by the rationalizing factor…

(2)   \begin{equation*} {S}_{yy}(\omega)-s^2{S}_{xx}(\omega) - \sqrt{[{S}_{yy}(\omega)-s^2{S}_{xx}(\omega)]^2 + 4s^2|{S}_{xy}(\omega)|^2}} \end{equation*}

…we can arrive at the following equation:

(3)   \begin{equation*} \hat{H}_{s}(\omega) = \frac{2S_{xy}(\omega)}{S_{xx}(\omega)-\frac{1}{s^2}S_{yy}(\omega)+\sqrt{[S_{xx}(\omega)-\frac{1}{s^2}S_{yy}(\omega)]^2+4\frac{1}{s^2}|S_{xy}(\omega)|^2}} \end{equation*}

Moreover, if we divide the numerator and denominator by s², we get:

(4)   \begin{equation*} \hat{H}_{s}(\omega) = \frac{2s^2S_{xy}(\omega)}{s^2S_{xx}(\omega)-S_{yy}(\omega)+\sqrt{[s^2S_{xx}(\omega)-S_{yy}(\omega)]^2+4s^2|S_{xy}(\omega)|^2}} \end{equation*}

Special Cases

Ĥ1, Ĥ2, and Ĥv are special cases of the scaled transfer function estimator. Using the definition of Ĥs, we see:

  • Ĥs=0 = Ĥ2
  • Ĥs=1 = Ĥy

Using the second alternate form, we see that Ĥs→∞ = Ĥ1.

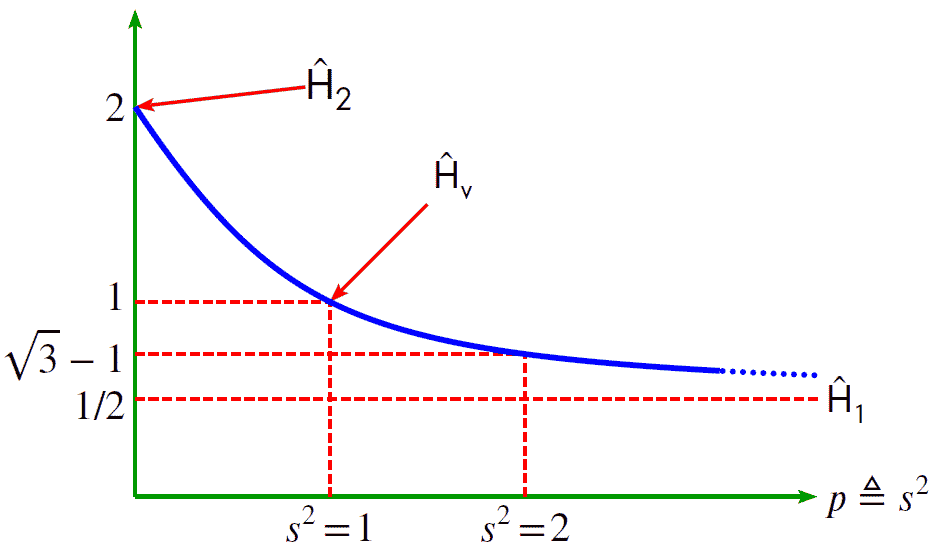
Transfer function, H, vs. the scaling factor, s, squared

Figure 1.5. Transfer function, H, vs. the scaling factor, s, squared.

MATLAB® Resources

pwelch(…)

Estimate power spectral density.

https://www.mathworks.com/help/signal/ref/pwelch.html

   

cpsd(…)

Estimate cross power spectral density.

https://www.mathworks.com/help/signal/ref/cpsd.html

Example of MATLAB Code

  clear                     % clear all variables
  format long g;            % set format of text output
  N       = 16;             % length of input data sequence
  Fs      = 1;              % sample rate (used for scaling)
  percent = 50;             % percent overlap
  Nfft = N * (1-percent/100);
  x= [0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0]';
  y= [0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0]';
%---------------------------------------------------------------------------
% smoothing window
%----------------------------------------------------------------------------
  window = hanning(Nfft);   % Hanning     window
%----------------------------------------------------------------------------
% calculate estimates
%----------------------------------------------------------------------------
[Syx,freq]=cpsd(  x,y,window,Noverlap,Nfft,Fs);      % estimate Syx
[Sxx,freq]=pwelch(x,  window,Noverlap,Nfft,Fs);      % estimate Sxx
[Syy,freq]=pwelch(  y,window,Noverlap,Nfft,Fs);      % estimate Syy>
% |     |     |   | |   |       |       |   |_________ sample rate
% |     |     |   | |   |       |       |_____________ estimate length
% |     |     |   | |   |       |_____________________ num. overlapping positions
% |     |     |   | |   |_____________________________ window type
% |     |     |   | |_________________________________ data sequence y
% |     |     |   |___________________________________ data sequence x
% |     |     |_______________________________________ estimation operation
% |     |_____________________________________________ x-axis sequence
% |___________________________________________________ estimate sequence
%----------------------------------------------------------------------------
% estimate scaling parameters
%----------------------------------------------------------------------------
  s = var(y)/var(x) % this is 'not' a recommended way to estimate s!
%----------------------------------------------------------------------------
% estimate Hs
%----------------------------------------------------------------------------
  Hs = estimate_Hs(s,Sxx,Syy,Sxy);
%----------------------------------------------------------------------------
% function to estimate Hs
%----------------------------------------------------------------------------
function Hs = estimate_Hs(s,Sxx,Syy,Sxy)
   u1 = Syy;
   u2 = s * Sxx;
   u3 = (s * Sxx - Syy) .* (s * Sxx - Syy);
   u4 = abs(Sxy) .* abs(Sxy);
   v1 = 2.0 * Sxy;
   Hs = (u1 - u2 + sqrt(u3 + 4 * s * u4)) ./ v1;
end