Probability Distribution of Random Vibration

Back to: Introduction to Vibration Signals

The probability density function (PDF) is another statistic that helps analyze random vibration and illustrates the range of acceleration values. With an acceleration waveform such as a PSD, random acceleration values may appear to be nearly the same. In such instances, the PDF can specify the probability of a random variable falling within a particular range of values rather than a single value.

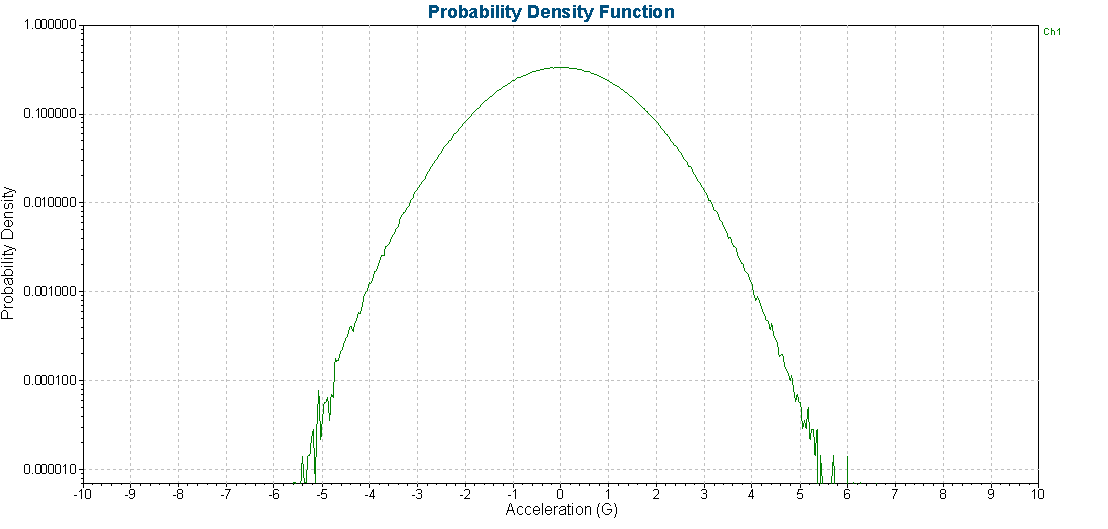
The PDF is an amplitude histogram that represents the probability of different acceleration values for a digitized signal. Each point in the histogram indicates the number of times the signal was within a small range of amplitudes. This range is often called the amplitude “bin.” The area under the PDF curve is always equal to 1, but the range of amplitude values depends on the width of each bin.

Probability Distribution

Random vibration displays a Gaussian (or normal) distribution. This distribution is commonly known as the bell curve. The weight of distribution is determined by several properties of the signal known as “moments.”

Signal Moments

The first moment is the mean value of the signal (μ), which must equal to zero for random shaker control; the second is variance (σ²), which is the squared deviation of a random variable from the mean; the third is skew, which indicates a bias towards larger positive or negative values; lastly, kurtosis, which measures high acceleration values.

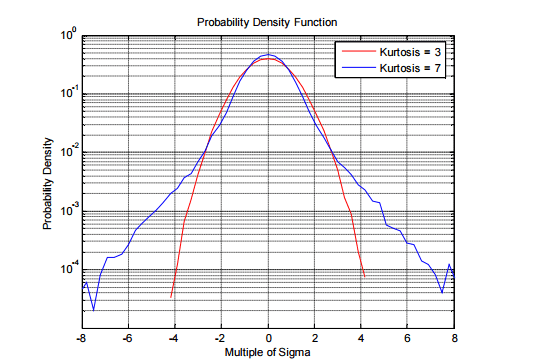
Kurtosis is a unitless parameter that quantifies the shape of a statistical distribution relative to Gaussian distribution. A Gaussian distribution has a kurtosis value of three. The higher the distribution of a peak, the more positive the kurtosis value; the flatter the kurtosis peak, the more negative the kurtosis value.

Practical testing only considers random motion bound by a crest factor, which is expressed as a ratio between the absolute maximum of the signal and the root-mean-square (RMS) value. The crest factor can be determined based on the test’s desired kurtosis value.

RMS vs. Peak

The PDF uses the unit G peak rather than RMS. RMS is a convenient measurement of the overall strength of a signal; however, peak accelerations can cause the most significant damage to a product.

Gaussian Distribution

Modern vibration controllers assume a Gaussian distribution of data, so the peak accelerations produced in a test are about three times the average acceleration value (kurtosis = 3). For many signals, nearly one hundred percent of the area of the curve (99.73%) is bounded by ±3σ.

However, peak accelerations found on the field can exceed three times the average acceleration. Assuming a Gaussian distribution removes the potentially damaging high peak accelerations and can result in under-testing. When a test spends less time near peak values, it can significantly reduce the amount of fatigue damage caused relative to the damage that the product will experience in the real world.

Thus, the current methods of random testing can be unrealistic in some situations because they do not include an environment’s most damaging content. Additionally, a random test with Gaussian distribution has a longer time-to-failure because the higher accelerations have been omitted.

Kurtosis Control

In vibration testing, the kurtosis value in a random vibration testing signal may be increased to generate a test that more closely reflects real-world vibration. To improve the accuracy of random testing, Vibration Research suggests that technicians determine the kurtosis value of their sample data and use it in their laboratory tests.

Kurtosis control methods, such as Vibration Research’s Kurtosion, are discussed in depth in the paper, “The Missing Knob on Your Random Vibration Controller.”

Sigma Clipping

A test engineer can manipulate a signal by “clipping” a Gaussian signal at a defined value. Clipping may be performed to increase the overall RMS of a test without having peaks that exceed the limits of a shaker. However, Vibration Research does not suggest using clipping as it is not necessary for most circumstances.