FIR-IIR Filter Comparison

Back to: Fundamentals of Signal Processing

Under the constraint of a polynomial-based filter structure, there are two common filter architectures: finite impulse response (FIR) and infinite impulse response (IIR).

A filter’s impulse response is its response to an input impulse, which is a theoretical signal. An IIR filter’s impulse response is “infinite” because it is indefinite; unlike an FIR filter response, it does not fall to zero.

FIR Filters

The FIR filter is a single polynomial. It is the weighted sum of the current input and a finite number of past inputs.

Advantages

• Extremely stable
• Can be designed to have a linear phase
• Has a finite impulse response: the output will go to exactly zero within a fixed time of the input going to zero

Disadvantages

• Tends to introduce long latency into the signal-processing chain
• Commonly requires many mathematical operations per input data sample (high computation)

IIR Filters

The IIR filter is a polynomial divided by a polynomial (a rational expression). It is the weighted sum of the current input, a finite number of past inputs, and a finite number of past outputs.

Advantages

• Stable if properly designed but possibly unstable if poorly designed
• Typically requires few mathematical operations per input data sample
• Can be designed to have a linear phase

Disadvantages

• Generally has a non-linear phase
• Has an infinite impulse response: generally and theoretically, the output will never reach exactly zero once excited with an input due to the feedback from the output

Example

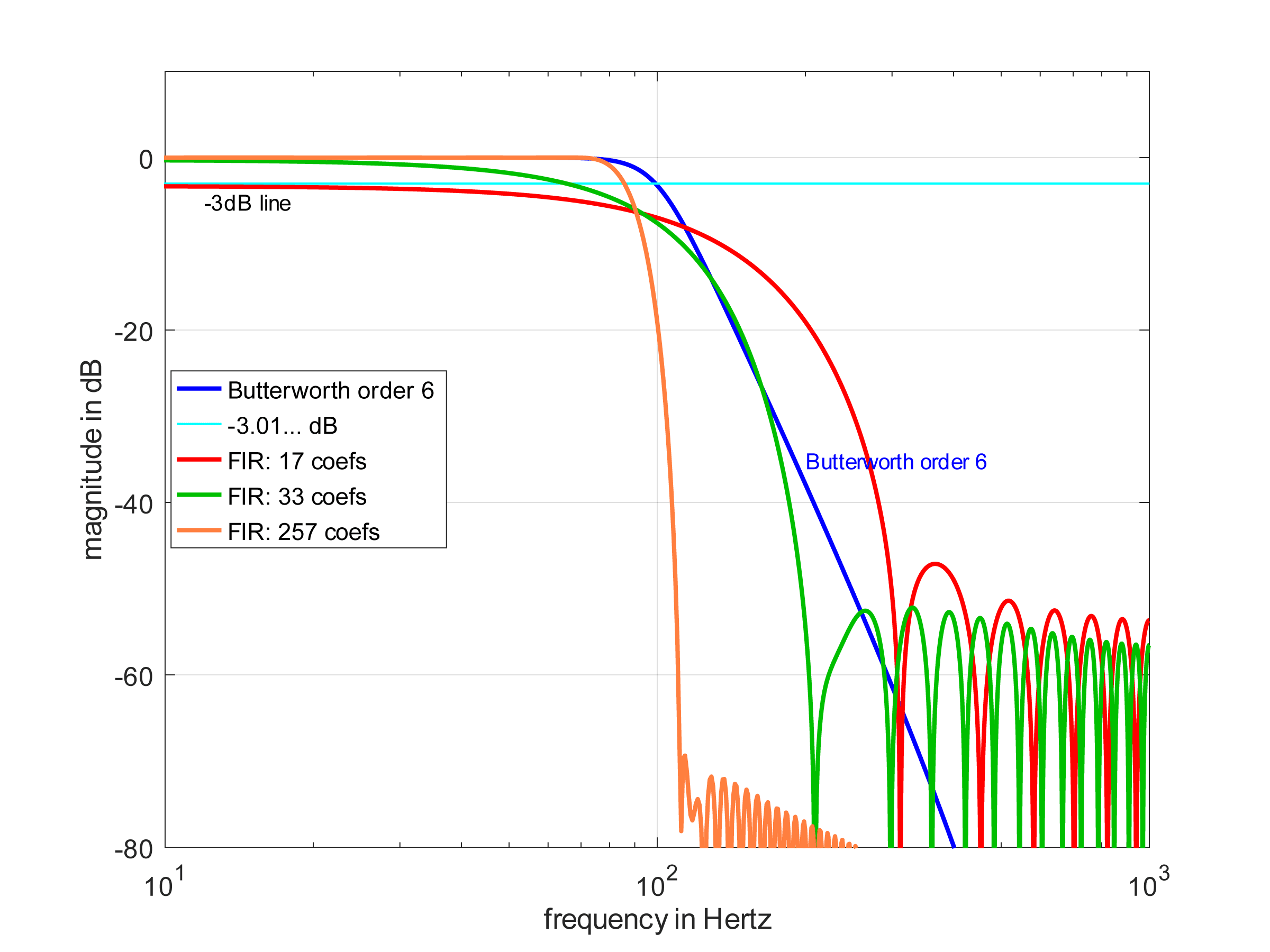
The example below compares an IIR Butterworth 6th order to FIR filters with 17, 33, and 257 coefficients. All have a target corner frequency of 100Hz. Observe the following:

• The 17 coefficient FIR under-performs the 13–15 coefficient Butterworth.
• The 33 coefficient FIR is more-or-less comparable to the Butterworth.
• The 257 coefficient FIR outperforms the Butterworth in terms of roll-off.

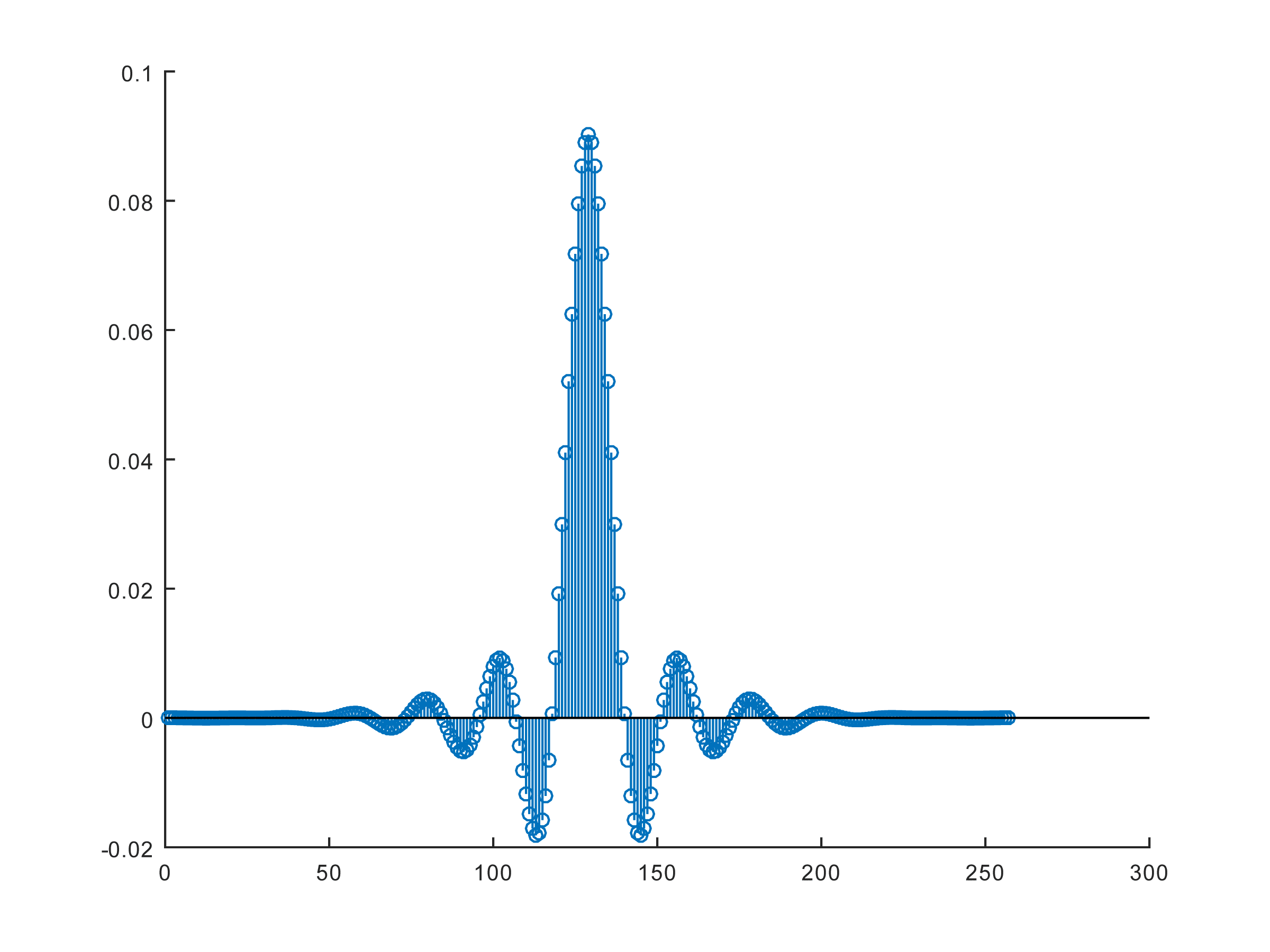
An FIR filter with many coefficients introduces a significant delay in the signal processing path as illustrated in the 257-coefficient FIR below.

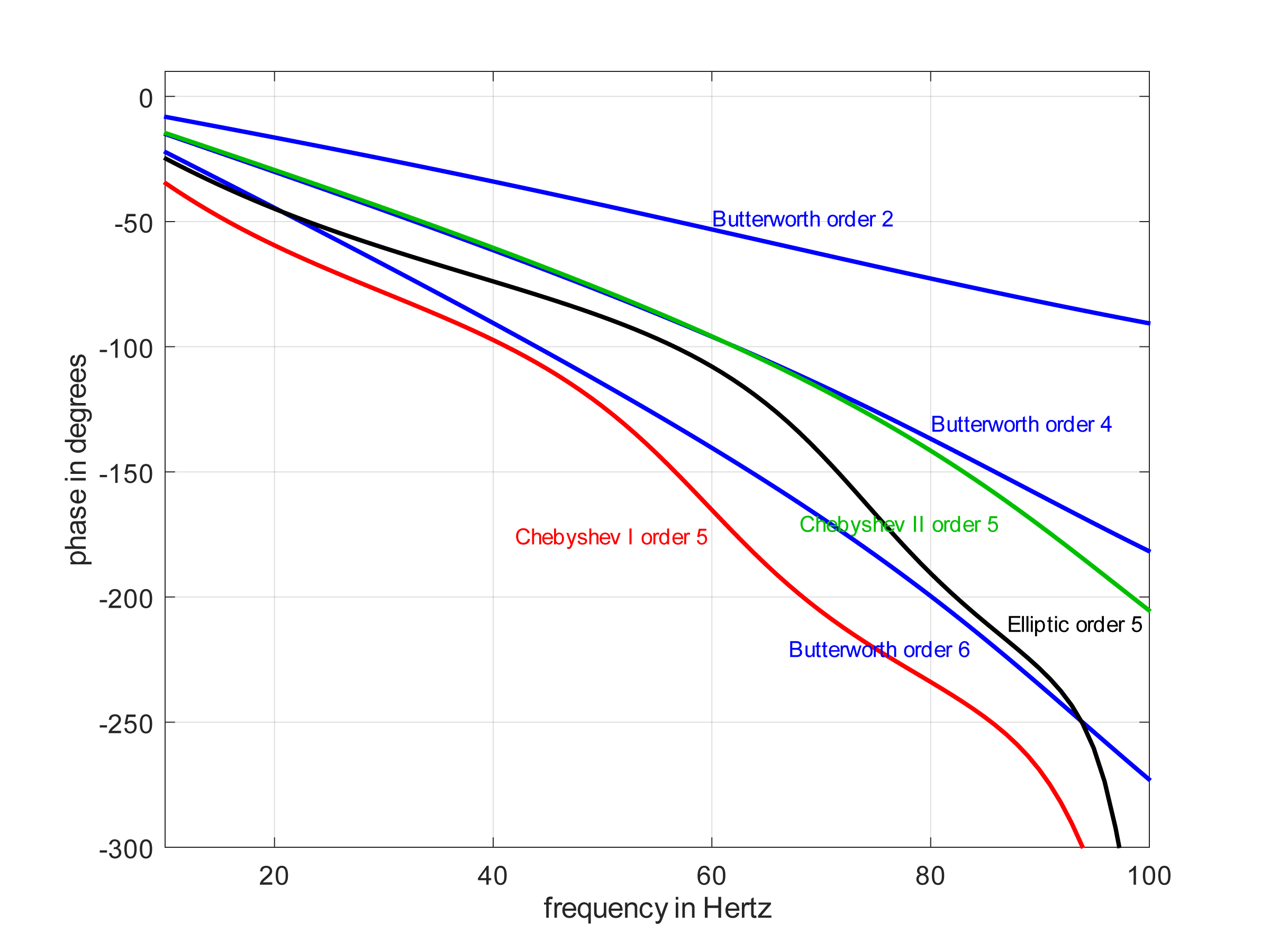
FIR filters can easily be designed to have a linear phase. For example, all FIR filters with symmetric coefficients have a linear phase (as illustrated above).

This is not the case with IIR filters, as illustrated in the IIR phase responses below. However, the Butterworth filter phase responses are approximately linear.