FFT and Window Functions
November 8, 2018
Back to: Window Functions for Signal Processing
Vibration test engineers seldom use raw time-domain data for analysis and identification. Typically, they employ signal processing to manipulate a vibration signal, sorting out relevant data or reducing external factors, such as noise. Signal processing helps produce clean data for identifying the behavior of a device under test (DUT).
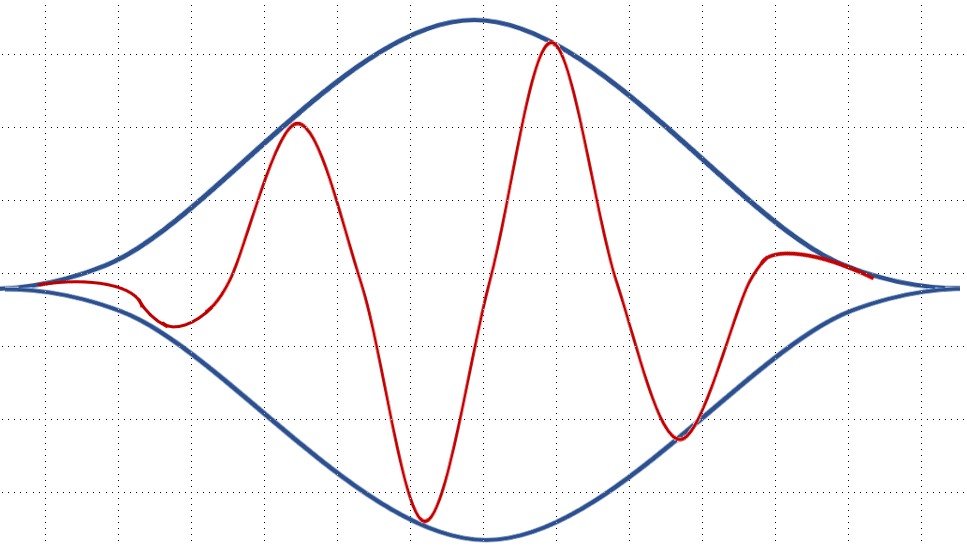
Figure 1.1. Applying a window function to a time-domain signal.
Windowing is a signal processing method engineers apply to a signal of a defined length to minimize discontinuities at its edges. This method multiplies a signal by a window function of a user-defined width, smoothing the signal’s amplitude at its edges towards zero.
Windowing is particularly relevant to vibration test engineers when discussing the fast Fourier transform (FFT).
FFT and Vibration Signal Processing
The FFT calculation is essential to signal processing. Digital signal processors can move data from the time domain into the frequency domain by performing a series of FFT calculations on frames of a signal, which are equal-sized sections of data.
However, the FFT assumes signals have an infinite, circular topology. It considers the two endpoints of the signal to be connected, meaning each end of the time interval has the same value. This assumption does not reflect a real-world random signal, and the resulting discontinuities in the time domain create unwanted noise in the frequency spectrum, known as spectral leakage. Engineers can apply a window function to the data frames to address these discontinuities (Figure 1.2).
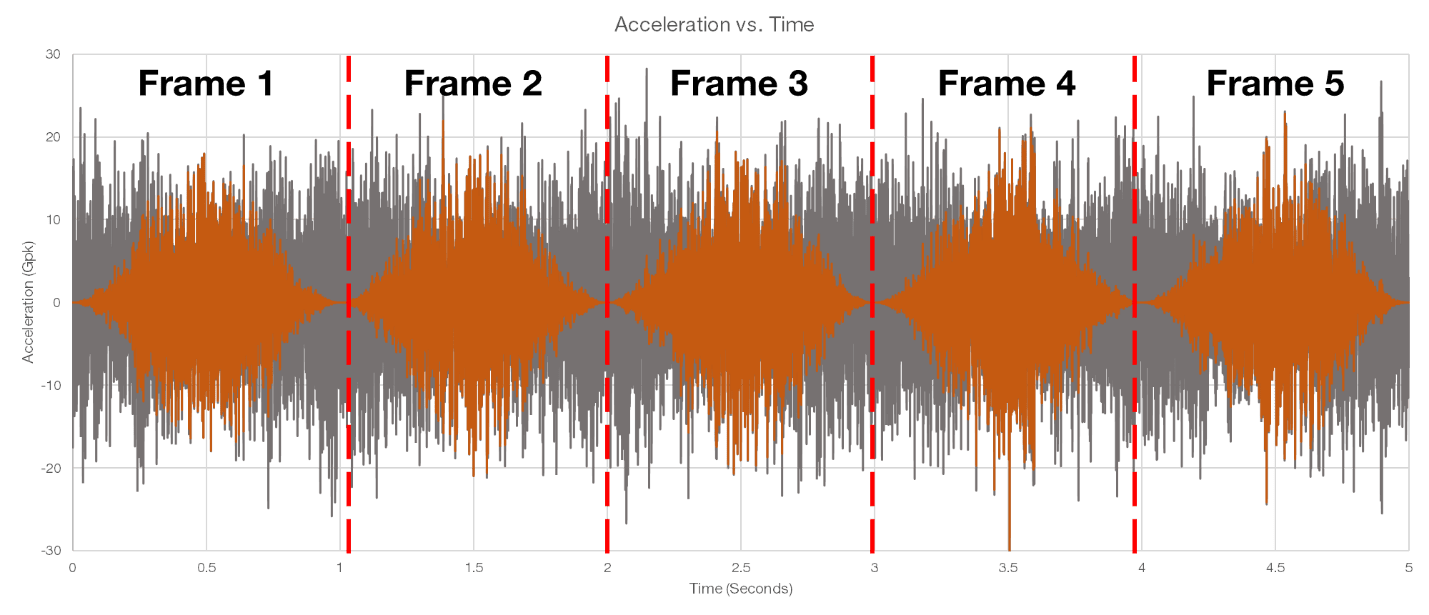
Figure 1.2. Windowed frames of a time-domain waveform before applying the FFT calculation. The gray waveform is the original data, and the orange signal is the windowed data.
Discontinuities in the Time Domain
Engineers apply window functions to a signal processing algorithm to address discontinuity, but this application does not overcome the discontinuity. Window functions multiply the time waveform by a finite-length window, which has an amplitude that varies smoothly and gradually toward zero at the edges. However, the multiplication in time results in a distortion in frequency. While the FFT of the windowed waveform will be similar to that of the original, it will have been altered.
Heisenberg Uncertainty Principle
In general, for a given window function, the larger the window in time (the more FFT analysis lines), the less distortion in frequency. The Heisenberg uncertainty principle summarizes this idea. Increasing the resolution in time (smaller window) decreases the resolution in frequency (more distortion). Conversely, decreasing the resolution in time increases the resolution in frequency.
Each window function generates different distortion characteristics for a given window size (or number of analysis lines). All window functions are defined in time and frequency. The characteristics of the resulting distortion depend on the definition of the selected window function.
Mathematicians and data scientists have developed a range of window functions. The following lessons explore the characteristics of these functions and how they differ.
