Undersampling and Aliasing
August 8, 2019
Sampling
Frequency Domain Consequences of Sampling
Reconstruction Via Interpolation
Quantization noise and over-sampling
Differential Quantization / Delta Modulation
Noise Shaping / Delta-Sigma Modulation
Back to: Sampling & Reconstruction
As discussed in the previous lesson, sampling at less than the Nyquist rate is called undersampling. When multiple copies of the signal in the DTFT frequency domain overlap, it may cause what is known as aliasing. When aliasing occurs, a high-frequency component will take on the alias of a different low-frequency component.
Frequency Content of Undersampled Waveform (Ex. 7)
Given the time waveform illustrated in Figure 2.1:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} x(t)=\frac{1}{\sqrt{2\pi}}\left[\frac{sin(t/2)}{t/2}\right]^2 \triangleq \frac{1}{\sqrt{2\pi}}sinc^2\left(\frac{t}{2}\right) \end{equation*}](https://vru.vibrationresearch.com/wp-content/ql-cache/quicklatex.com-8c2ba5711fefbe1059d04a88ca0d1d01_l3.png)
The Fourier transform 𝖷̃(𝜔) is the triangle function illustrated in Figure 2.6, where the highest frequency component is 𝖿h = 1/2𝜋 Hz.
The waveform x(t) sampled at 𝖥s ≜ 1 × 𝖿h = 1/2𝜋 gives a sample period of 𝜏 = 1/𝖥s = 2𝜋 and is illustrated in Figure 2.9. It is an example of undersampling.

Figure 2.9. An undersampled sequence.
All the samples are zero, aside from the center sample at t=0. This sequence results in a DTFT that is constant across frequency 𝜔.
Using the same sample rate and applying Theorem 1 results in a DTFT 𝖸̃(𝜔) of y(n) that will overlap, or alias, in the DTFT’s frequency domain. It is expressed as:
(2) ![]()
(3) ![Rendered by QuickLaTeX.com \begin{equation*} =\frac{\sqrt{2\pi}}{2\pi}\sum_{n\in\mathbb{Z}}\tilde{X}\left(\frac{1}{2\pi}[\omega-2\pi n]\right) \end{equation*}](https://vru.vibrationresearch.com/wp-content/ql-cache/quicklatex.com-b05b3eef67087a57dd7615d7c77b4414_l3.png)
Conclusion
- 𝖷̃(𝜔) repeats every 2𝜋 (this is true of all DTFTs)
- 𝖷̃(𝜔) is 0 when (1/2𝜋) 𝜔 = 1…that is, at 𝜔 = 2𝜋
- The height of each triangle is
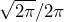 or about 0.399
or about 0.399 - The spectral content is a constant (displayed as the solid red line in Figure 2.10 below)

Figure 2.10. Undersampled DTFT.
