Statistical Analysis
June 2, 2021
Back to: Fundamentals of Signal Processing
Statistical analysis takes a random variable and conveys its likely characteristics.
Specifically, it characterizes random sample(s) drawn from a probability space (Ω, E, P) in terms of non-random statistics. Often, these statistics are defined in terms of the expectation operator E.
The expectation operator creates a map from a random variable to a specific number like 2.7 or 5. The statistics can be calculated analytically if the probability function P in (Ω, E, P) is known. However, in the real world, P usually isn’t known. In such cases, statistics may be estimated with various techniques.
Here are several takeaways about statistical analysis:
- Statistical analysis is performed on a random variable or random process.
- A random variable turns an experimental outcome into a number.
Random & Non-random Numbers
Random variables in the form of numbers allow engineers to perform mathematical operations on random variables. However, a mathematical operation on a random number is still a random number.
Before a decision can be made, engineers require a non-random number (statistic) that tells them about the underlying physical system that generated the random number. Typically, the operation that maps a random number (variable) to a non-random number is the expectation operator E.
Expectation Operator E
The expectation operator E is at the foundation of many statistics and statistical analyses. The expectation EX of a random variable X is the sum of each possible value of X weighted by the probability of the value occurring.
The expected value EX of a random variable X is:
(1) ![]()
where […, x1, x2, x3, x4, x5, …] are the possible values of X and P(xn) is the probability that the value xn will occur.
The expected value EX tells an engineer what to expect from X.
Example
If X is a random variable that represents the sum of a pair of dice, then the expected value EX of X is:
EX = 2(1/36) + 3(2/36) + 4(3/36) + … + 12(1/36) = 7
Therefore, we might expect a pair of dice to come up with a sum of 7.
Moments of Single Random Variables
Using the expectation operator, we can define some common statistics, or moments, of a single random variable X.
- The nth moment of X is E[Xn].
- The 1st moment is the mean or μ.
- The nth absolute moment of X is E[|X|n]. E[|X|2] is closely related to the Welch estimate of the PSD.
The nth central moment of X is E[(X-μ)n].
-
- E[(X-μ)2] is the variance of X or σ².
- E[(X-μ)3] is the skewness of X.
- E[(X-μ)4] is the kurtosis of X.
The nth absolute central moment of X is E[|X-μ|n].
Example: Moment Statistics
Using the dice pair example above:
(2) ![]()
(3) ![]()
(4) 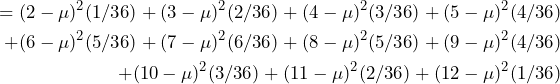
(5) ![]()
(6) ![]()
In this example, μ and σ² were calculated from the known probability function P. However, in most real-world applications, P is not known. In this case, the common solution is to take many samples and estimate statistics from them.
Arithmetic Mean
The arithmetic mean can be used when estimating the mean μ=E[X]. The arithmetic mean of the samples x1, x2, x3, …, xN; is defined as:
(7) ![]()
Is the arithmetic mean a good estimate of the true mean E[X]? The answer depends on how large N is and if the device that generated the samples is stable over time (if the process is wide-sense stationary or WSS).
If N is large and the process is WSS, then the arithmetic mean is, informally, a good estimate of E[X]. For example, the engineer can say the estimate is unbiased.
(1/N) times the sum of N random variables is a random variable:
(8) ![]()
The expected value of Y is:
(9) 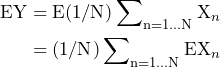
If the process is wide-sense stationary, then EXn are all the same and:
(10) 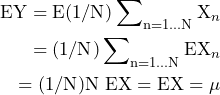
The expected value of the arithmetic mean is the true mean. This means that the arithmetic mean is an unbiased estimate of the true mean.
