Resonance
June 2, 2021
Back to: Fundamentals of Signal Processing
A PSD Sxx(f) or a transfer function H(f) can be used to find a resonance or an anti-resonance in a system.
Resonance at a resonant frequency f is a pronounced increase in the magnitude of H in the vicinity of f, and an anti-resonance is a pronounced decrease.
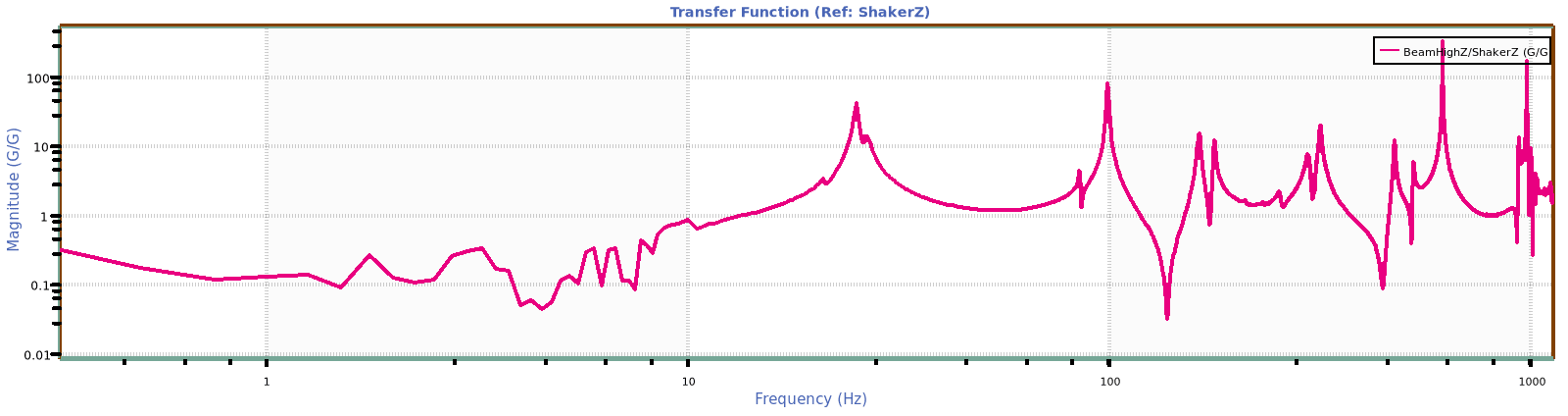
Resonance is often the result of energy at frequency f reflecting within a device through multiple paths and adding constructively (“resonating”) to produce an increase in spectral power in the vicinity of the resonance frequency. The frequency at which a device resonates is a direct result of the physical dimensions of the device.
Resonance is sometimes a desirable effect, and other times not so much. The same can be said for anti-resonance.
Examples
An example of a desirable resonance is that which occurs in guitar and piano strings. Parabolic radar and TV satellite dish antennas are also desirable resonances. An undesirable resonance may occur in car tires with poorly designed tread patterns that result in unwanted road noise.
Desirable anti-resonances include active noise cancellation systems in personal headphone devices that reduce the low-frequency rumble heard on airliners. An undesirable anti-resonance may be a speaker cone for a home entertainment system, as the speakers would ideally have a flat response in their specified frequency range.
