CoursesCertificatesBack to VR.com

MENU

DSP Calculus

June 2, 2021

Back to: Fundamentals of Signal Processing

In many cases, the physical world is ruled by differential relationships. For example:

  • Velocity = d/dt displacement
  • Acceleration = d/dt velocity
  • Current through a capacitor = capacitance (C) times d/dt of the voltage across the capacitor

Digital Differentiation

Differentiation (d/dt) is built for the analog world or continuous functions, not for the digital signal processor (DSP) one (discrete functions or sequences). By definition:

(1)   \begin{equation*} \frac{d}{dt}x(t)=\lim_{h\to0}\frac{x(t)-x(t-h)}{h} \end{equation*}

If x(t) is continuous, then x(t) and x(t-h) can get closer while h gets closer to 0. However, if x(n) is discrete, then the smallest h can be is 1, and the closest the numerator can get is x(n)-x(n-1).

That is, the resolution of digital differentiation is limited by the sample rate Fs.

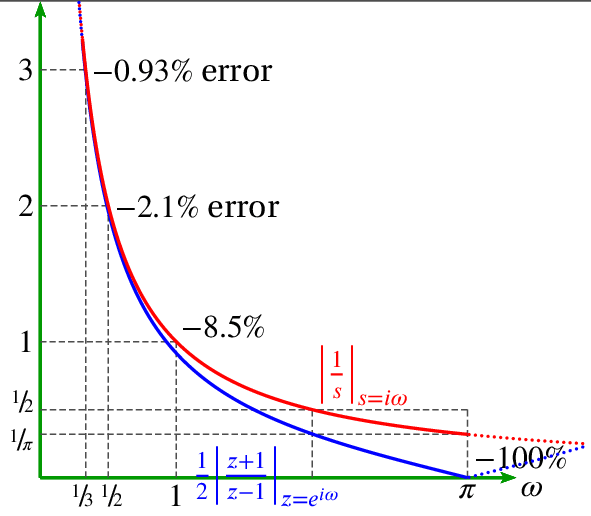
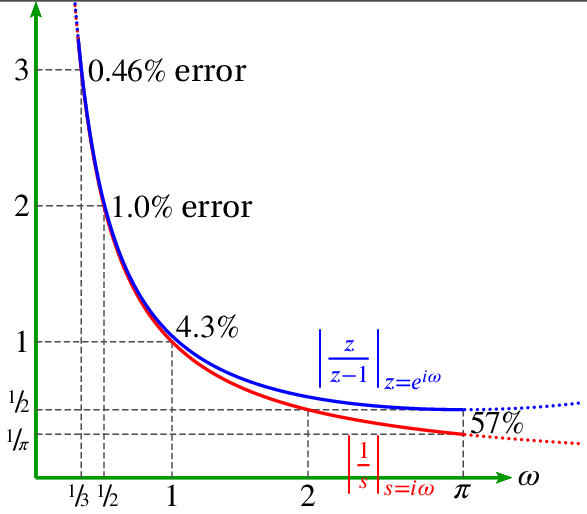
How accurate is discrete differentiation compared to continuous differentiation? It is helpful to compare them in the frequency domain.

The Fourier transform of d/dt is iω because:

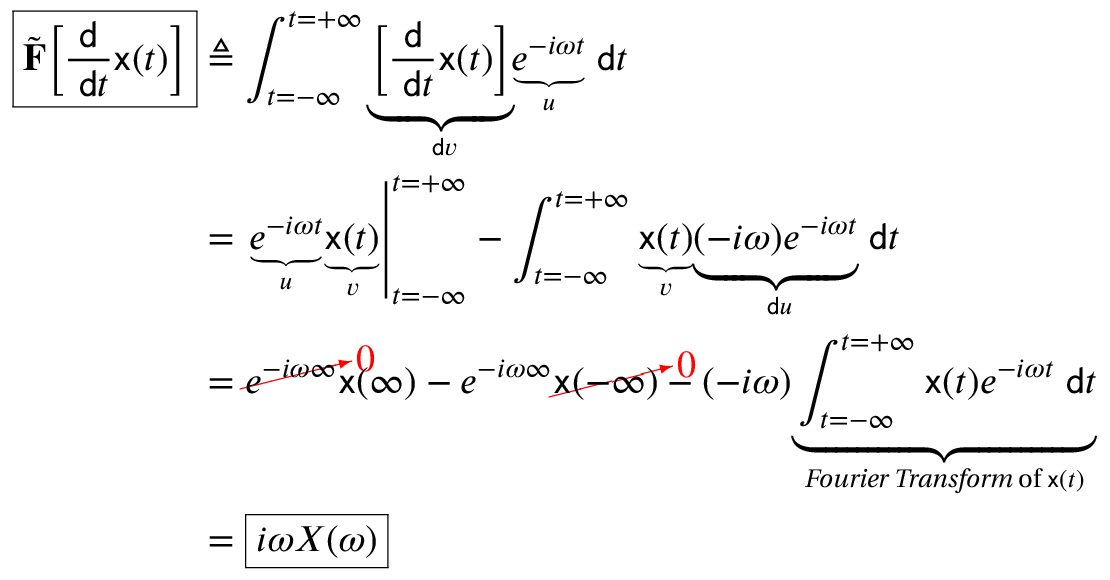
Fourier transform of d/dt

The z-transform of y(n)=x(n)-x(n-1) is Y(z) = X(z) – z-1X(z). Therefore:

(2)   \begin{equation*} \frac{Y(z)}{X(z)}=1-z^{-1}=\frac{z-1}{z} \end{equation*}

For the DFT, z=eiω. Therefore, the z-transform of y(n)=x(n)-x(n-1) is Y(z) = X(z) – z-1X(z) and:

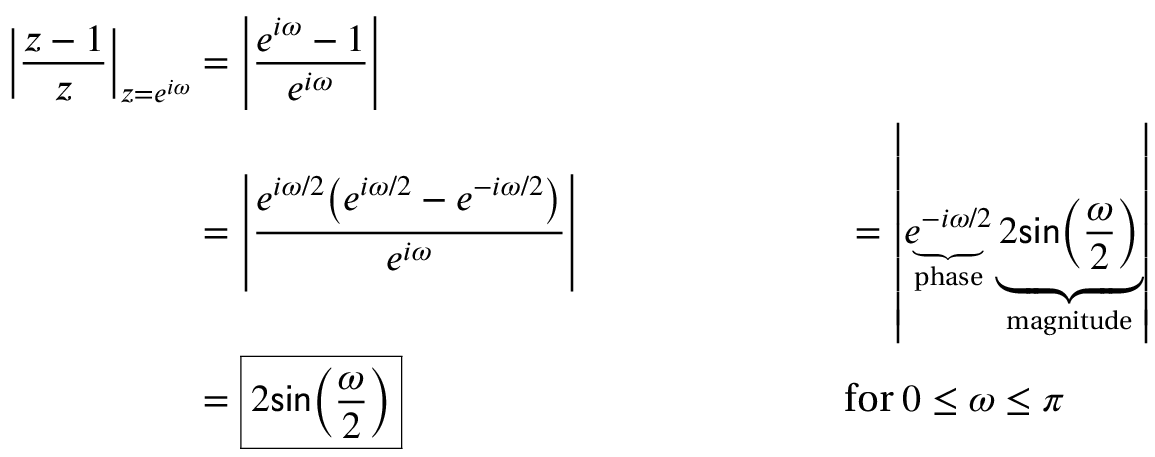
z-transform of y(n)=x(n)-x(n-1)

We can plot the magnitudes of both to compare them:

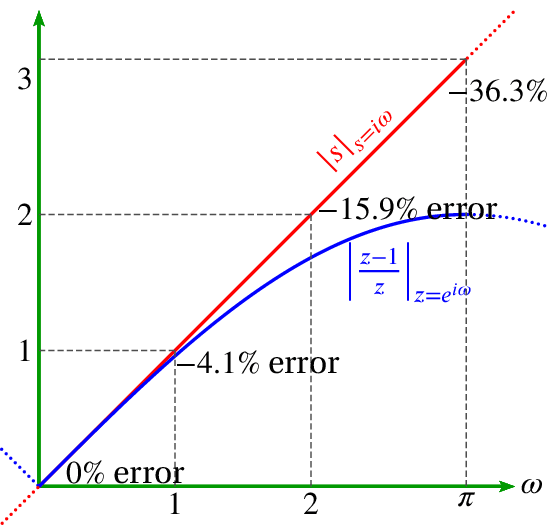
Comparison of Fourier transform and z-transform differentiation methods

Note that digital differentiation is more accurate at lower frequencies.

Digital Integration

A similar analysis can be performed for integration. Here, the Fourier transform is -i/iω. The two digital methods are integration using summation and integration using the trapezoid rule.

Integration using Summation

Integration using summation

Integration using Trapezoid Rule

Integration using trapezoid rule